Tính nguyên hàm của 1/x^3+x^2-22x-40
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án B.
Đặt t = 2 x − 1 ⇒ t 2 = 2 x − 1 ⇒ t d t = d x
⇒ F x = ∫ 2 2 x − 1 d x = ∫ 2 t t d t = 2 t + C = 2 t + C = 2 2 x − 1 + C .
F 5 = 7 ⇔ 2 2.5 − 1 + C = 7 ⇒ C = 1 ⇒ f x = 2 2 x − 1 + 1.

Ta có: f ( x ) = 2 2 x = 4 x nên nguyên hàm của f(x) là 4 x ln 4 + C
Chọn đáp án A.
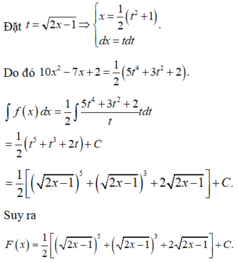
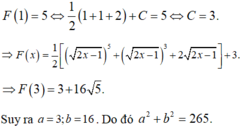
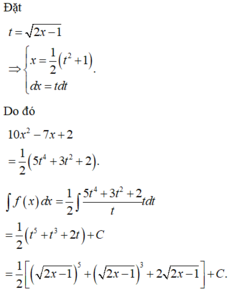
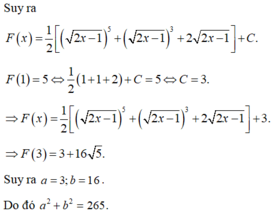
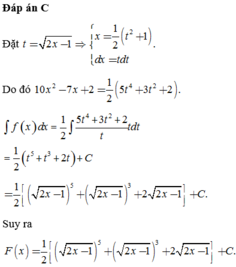

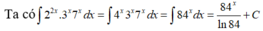
\(\int\dfrac{1}{x^3+x^2-22x-40}dx=\int\dfrac{1}{\left(x-5\right)\left(x+2\right)\left(x+4\right)}dx\)
\(=\int\left(\dfrac{1}{63}.\dfrac{1}{x-5}-\dfrac{1}{14}.\dfrac{1}{x+2}+\dfrac{1}{18}.\dfrac{1}{x+4}\right)dx\)
\(=\dfrac{1}{63}ln\left|x-5\right|-\dfrac{1}{14}ln\left|x+2\right|+\dfrac{1}{18}ln\left|x+4\right|+C\)