Cho tam giác ABC cân ở A,đường cao BH=5cm,ABH=30độ .Giải tam giác ABC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(S_{\Delta BAC}=S_{\Delta BHA}+S_{\Delta BHC}=40+S_{\Delta BHC}\Rightarrow S_{\Delta BHC}=10\left(cm\right)\)(vô lý)

Tam giác ABC cân tại A nên AB = AC , góc B = góc C
Xét tam giác ABH và ACH có :
góc B = góc C ; AB = AC ; Góc BAH = CAH ( vì AH là tia phân giác của góc A )
=> tam giác ABH = tam giác ACH ( g.cg )
=> BH = CH ( hai cạnh tương ứng )
=> H là trung điểm của BC. => AH là đường đường trung tuyến của tam giác ABC .
d, Vì tam giác ABH = tam giác ACH => góc BHA = góc CHA (1) ( 2 góc tương ứng )
ta lại có : góc BHA + góc CHA = 180 độ (2) ( hai góc kề bù )
Từ (1) và (2) suy ra góc BHA = góc CHA = 90 độ => tam giác AHB vuông tại H
áp dụng định lí Pytago cho tam giác vuông AHB ta có : \(AB^2=AH^2+HB^2\Rightarrow AH^2=AB^2-HB^2.\)
=> \(AH=\sqrt{AB^2-HB^2}=\sqrt{13^2-5^2}=12\)(cm)

b: \(BH=\dfrac{5\sqrt{3}}{3}\left(cm\right)\)
a: Đề sai rồi bạn
a.=> BC = BH + CH = 1 + 3 = 4 cm
áp dụng định lý pitago vào tam giác vuông AHB
\(AB^2=HB^2+AH^2\)
\(AB=\sqrt{1^2+2^2}=\sqrt{5}cm\)
áp dụng định lí pitago vào tam giác vuông AHC
\(AC^2=AH^2+HC^2\)
\(AC=\sqrt{2^2+3^2}=\sqrt{13}cm\)

1: Xet ΔABH vuông tại H và ΔCAH vuông tại H có
góc ABH=góc CAH
=>ΔABH đồng dạng với ΔCAH
=>HA/HC=HB/HA
=>HA^2=HB*HC
2: AH=căn 4*9=6cm
AB=căn 4*13=2*căn 13(cm)

a: Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
góc BAH chung
Do đó: ΔAHB=ΔAKC
b: góc ABH+góc EBC=góc ABC
góc ACK+góc ECB=góc ACB
mà góc ABH=góc ACK;góc ABC=góc ACB
nên góc EBC=góc ECB
=>ΔEBC cân tại E
c: AB=AC
EB=EC
=>AE là trung trực của BC
=>AE vuông góc với BC


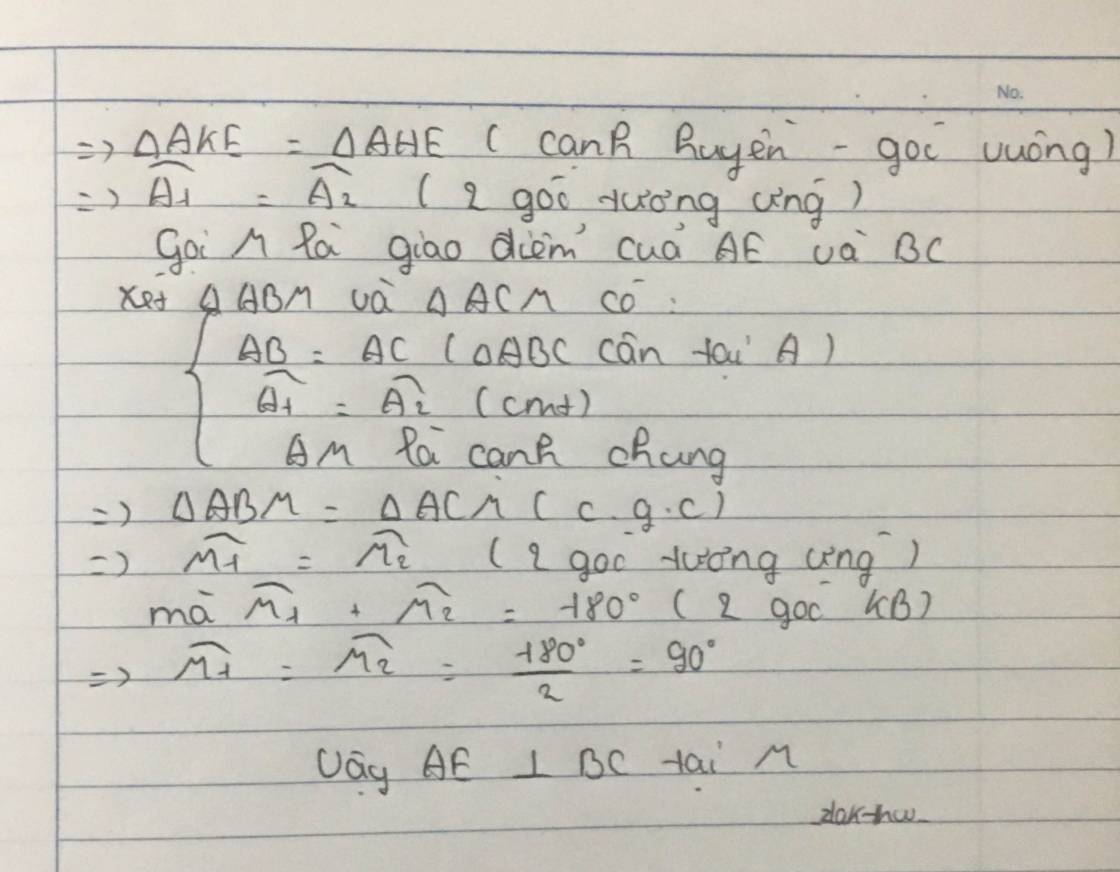
Tam giác ABH vuông tại H, có góc ABH = 300
=> góc A = 600
mà tam giác ABC cân tại A
=> tam giác ABC đều
=> góc B = góc C = 600
\(\tan A=\tan60^0=\frac{BH}{AH}=\sqrt{3}\)
=> \(AH=\frac{BH}{\sqrt{3}}=\frac{5}{\sqrt{3}}\)
do tam giác ABC đều, BH là đường cao
=> BH đồng thời là trung tuyến
=> \(AC=\frac{10}{\sqrt{3}}\)
Vậy \(AB=AC=BC=\frac{10}{\sqrt{3}}\); \(\widehat{A}=\widehat{B}=\widehat{C}=60^0\)