
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



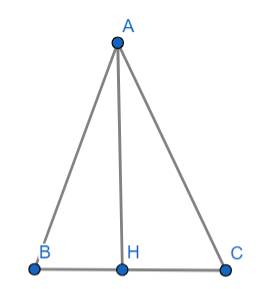
Xét tam giác vuông ABH vuông tại H ta có:
\(AB^2=BH^2+AH^2\)
\(\Rightarrow AH=\sqrt{AB^2-BH^2}\)
\(\Rightarrow AH=\sqrt{6^2-5^2}=\sqrt{11}\left(cm\right)\)
Mà tam giác ABC cân tại A nên \(BC=2BH=2\cdot5=10\left(cm\right)\)
Diện tích tam giác ABC là:
\(S_{ABC}=\dfrac{1}{2}\cdot AH\cdot BC=\dfrac{1}{2}\cdot10\cdot\sqrt{11}=5\sqrt{11}\left(cm^2\right)\)

Áp dụng định lý Pitago:
\(AB=\sqrt{AH^2+BH^2}=\sqrt{41}\)
Áp dụng hệ thức lượng:
\(AB^2=BH.BC\Rightarrow BC=\dfrac{AB^2}{BH}=\dfrac{41}{4}\)
Áp dụng Pitago:
\(AC=\sqrt{BC^2-AB^2}=\dfrac{5\sqrt{41}}{4}\)
Chu vi: \(AB+AC+BC=\dfrac{41+9\sqrt{41}}{4}\left(cm\right)\)

\(1,\)
\(a,\) Áp dụng HTL tam giác
\(\left\{{}\begin{matrix}AH^2=CH\cdot BH\\AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}BH=\dfrac{AH^2}{CH}=\dfrac{25}{6}\left(cm\right)\\AB=\sqrt{\dfrac{25}{6}\left(\dfrac{25}{6}+6\right)}=\dfrac{5\sqrt{61}}{6}\left(cm\right)\\AC=\sqrt{6\left(\dfrac{25}{6}+6\right)}=\sqrt{61}\left(cm\right)\end{matrix}\right.\\ BC=\dfrac{25}{6}+6=\dfrac{61}{6}\left(cm\right)\)
\(b,S_{ABC}=\dfrac{1}{2}AH\cdot BC=\dfrac{1}{2}\cdot5\cdot\dfrac{61}{6}=\dfrac{305}{12}\left(cm^2\right)\)

Sửa đề: AH=12cm; AB<AC và BC=25cm
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH^2=HB\cdot HC\)
hay \(HB\cdot HC=12^2=144\)
Ta có: HB+HC=BC(H nằm giữa B và C)
nên HB+HC=25(cm)
Vì AB<AC nên HB<HC
mà HB+HC=25(cm)
nên \(\left\{{}\begin{matrix}HB< \dfrac{25}{2}=12.5\left(cm\right)\\HC>\dfrac{25}{2}=12.5\left(cm\right)\end{matrix}\right.\)
Ta có: HB+HC=25(cmt)
nên HB=25-HC
Ta có: \(HB\cdot HC=144\)(cmt)
nên \(\left(25-HC\right)\cdot HC=144\)
\(\Leftrightarrow25HC-HC^2-144=0\)
\(\Leftrightarrow HC^2-25HC+144=0\)
\(\Leftrightarrow\left(HC-16\right)\left(HC-9\right)=0\)
\(\Leftrightarrow HC=16\left(cm\right)\)
\(\Leftrightarrow HB=BC-HC=25-16=9\left(cm\right)\)
Vậy: HB=9cm; HC=16cm; \(S_{ABH}=54\left(cm^2\right)\)

\(a,BC=\sqrt{AB^2+AC^2}=13\left(cm\right)\\ HTL:\left\{{}\begin{matrix}AH=\dfrac{AB\cdot AC}{BC}=\dfrac{60}{13}\left(cm\right)\\BH=\dfrac{AB^2}{BC}=\dfrac{25}{13}\left(cm\right)\end{matrix}\right.\\ b,AM=\dfrac{1}{2}BC=\dfrac{13}{2}\left(cm\right)\left(trung.tuyến.ứng.cạnh.huyền\right)\\ \Rightarrow HM=\sqrt{AM^2-AH^2}=\dfrac{119}{26}\left(cm\right)\\ \Rightarrow S_{AHM}=\dfrac{1}{2}AH\cdot HM=\dfrac{1}{2}\cdot\dfrac{60}{13}\cdot\dfrac{119}{26}=\dfrac{1785}{169}\left(cm^2\right)\)

BÀI 1:
a)
· Trong ∆ ABC, có: AB2= BC.BH
Hay BC= ![]() =
= ![]()
· Xét ∆ ABC vuông tại A, có:
AB2= BH2+AH2
↔AH2= AB2 – BH2
↔AH= ![]() =4 (cm)
=4 (cm)
b)
· Ta có: HC=BC-BH
àHC= 8.3 - 3= 5.3 (cm)
· Trong ∆ AHC, có:

· ![]()
Bài 1:
a) Áp dụng hệ thức lượng ta có:
\(AB^2=BH.BC\)
\(\Rightarrow\)\(BC=\frac{AB^2}{BH}\)
\(\Rightarrow\)\(BC=\frac{5^2}{3}=\frac{25}{3}\)
Áp dụng Pytago ta có:
\(AH^2+BH^2=AB^2\)
\(\Rightarrow\)\(AH^2=AB^2-BH^2\)
\(\Rightarrow\)\(AH^2=5^2-3^2=16\)
\(\Rightarrow\)\(AH=4\)
b) \(HC=BC-BH=\frac{25}{3}-3=\frac{16}{3}\)
Áp dụng hệ thức lượng ta có:
\(\frac{1}{HE^2}=\frac{1}{AH^2}+\frac{1}{HC^2}\)
\(\Leftrightarrow\)\(\frac{1}{HE^2}=\frac{1}{4^2}+\frac{1}{\left(\frac{16}{3}\right)^2}=\frac{25}{256}\)
\(\Rightarrow\)\(\frac{1}{HE}=\frac{5}{16}\)
\(\Rightarrow\)\(HE=\frac{16}{5}\)

Theo định lý Pytago :
\(AB^2+AC^2=BC^2\\ \Rightarrow BC=\sqrt{5^2+12^2}=13\left(cm\right)\)
Tam giác ABC vuông tại A
\(AB^2=BH.BC\\ \Rightarrow BH=\dfrac{AB^2}{BC}=\dfrac{5^2}{13}=\dfrac{25}{13}\left(cm\right)\)
\(AB.AC=AH.BC\\ \Rightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{5.12}{13}=\dfrac{60}{13}\left(cm\right)\)
\(AC^2=HC.BC\\ \Rightarrow HC=\dfrac{AC^2}{BC}=\dfrac{12^2}{13}=\dfrac{144}{13}\left(cm\right)\)
ΔABC vuông tại A
=>\(BC^2=AB^2+AC^2\)
=>\(BC=\sqrt{5^2+12^2}=13\left(cm\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\\AH\cdot BC=AB\cdot AC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH=\dfrac{5^2}{13}=\dfrac{25}{13}\left(cm\right)\\CH=\dfrac{12^2}{13}=\dfrac{144}{13}\left(cm\right)\\AH=\dfrac{5\cdot12}{13}=\dfrac{60}{13}\left(cm\right)\end{matrix}\right.\)
Tam giác ABH vuông tại H, có góc ABH = 300
=> góc A = 600
mà tam giác ABC cân tại A
=> tam giác ABC đều
=> góc B = góc C = 600
\(\tan A=\tan60^0=\frac{BH}{AH}=\sqrt{3}\)
=> \(AH=\frac{BH}{\sqrt{3}}=\frac{5}{\sqrt{3}}\)
do tam giác ABC đều, BH là đường cao
=> BH đồng thời là trung tuyến
=> \(AC=\frac{10}{\sqrt{3}}\)
Vậy \(AB=AC=BC=\frac{10}{\sqrt{3}}\); \(\widehat{A}=\widehat{B}=\widehat{C}=60^0\)