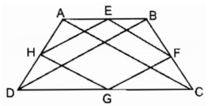
Cho hình bình hành ABCD. Gọi E, F, G, H theo thứ tự nằm trên cạnh AB, BC, CD, DA sao cho BE=DG; BF=DH. Chứng minh rằng:
a, EFGH là hình bình hành (câu này mình đã làm được rồi nhé!)
b, Bốn đoạn thẳng AC, BD, EG, FH đồng quy
Câu a mình làm được rồi, nên các bạn chỉ cần làm câu b giúp mình nhé!