Question

[Huỳnh Đạt]

Bài 1: Xác định m để hai đường thẳng (d): y= mx-4 và (d'): y= x+m cắt nhau tai 1 điểm thuộc:

a. Trục tung

b. Trục hoành

c. Cắt nhau tại điểm có tung độ bằng 1.

Bài 2: Cho đường thẳng (d): y= (m+1)x -m -3

a. Chứng tổ rằng (d) luôn đi qua 1 điểm với bất kỳ m nào.

b. Tìm m để đường thẳng (d) cắt hai trục tọa độ tai hai điểm A, B sao cho tam giác OAB vuông cân với O là gốc tọa độ.

Answer 1

[Akai Haruma]

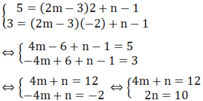
Bài 1:

Gọi giao điểm của 2 đths là \(I(x_I,y_I)\)

a)

Giao điểm nằm trên trục tung thì \(x_I=0\)

Ta có: \(I\in (d);(d')\Rightarrow \left\{\begin{matrix} y_I=m.0-4=-4\\ y_I=0+m=m\end{matrix}\right.\)

\(\Rightarrow m=-4\)

b) Giao điểm nằm trên trục hoành thì \(y_I=0\)

Ta có: \(I\in (d);(d')\Rightarrow \left\{\begin{matrix} 0=mx_I-4\\ 0=x_I+m\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} mx_I=4\\ x_I=-m\end{matrix}\right.\)

\(\Rightarrow -m^2=4\) (VL)

Vậy k tồn tại $m$ để hai đths cắt nhau tại một điểm trên trục hoành.

c)

Hai đths cắt nhau tại điểm có tung độ bằng $1$

\(\Leftrightarrow \left\{\begin{matrix} mx_I-4=1\\ x_I+m=1\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} mx_I=5\\ x_I=1-m\end{matrix}\right.\)

\(\Rightarrow m(1-m)=5\)

\(\Leftrightarrow (m-\frac{1}{2})^2+\frac{19}{4}=0\) (VL)

Vậy k tồn tại $m$ để 2 đths cắt nhau tại điểm có tung độ bằng $1$

Answer 2

[Akai Haruma]

Bài 2:

\(y=(m+1)x-m-3, \forall m\)

\(\Leftrightarrow m(x-1)+x-3-y=0, \forall m\)

Để điều này xảy ra thì \(\left\{\begin{matrix} x-1=0\\ x-3-y=0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x=1\\ y=-2\end{matrix}\right.\)

Như vậy $(d)$ luôn đi qua điểm \((1,-2)\) với mọi $m$

b) ĐK: \(m\neq -1\)

\(A=(d)\cap Ox\Rightarrow \left\{\begin{matrix} y_A=0\\ y_A=(m+1)x_A-m-3\end{matrix}\right. \)

\(\Rightarrow \left\{\begin{matrix} y_A=0\\ x_A=\frac{m+3}{m+1}\end{matrix}\right.\)

\(B=(d)\cap Oy\Rightarrow \left\{\begin{matrix} x_B=0\\ y_B=(m+1)x_B-m-3\end{matrix}\right.\)

\(\Rightarrow \left\{\begin{matrix} x_B=0\\ y_B=-m-3\end{matrix}\right.\)

Vì $A,B$ nằm trên trục hoành và trục tung nên hiển nhiên tam giác $OAB$ vuông sẵn. Vậy để nó là tam giác vuông cân thì $OA=OB$

\(\Leftrightarrow \sqrt{(\frac{m+3}{m+1})^2}=\sqrt{(-m-3)^2}\)

\(\Leftrightarrow (\frac{m+3}{m+1})^2=(m+3)^2\)

\(\Leftrightarrow (m+3)^2\left(\frac{1}{(m+1)^2}-1\right)=0\)

\(\Rightarrow \left[\begin{matrix} m=-3\\ m=-2\\ m=0\end{matrix}\right.\)

Với $m=-3$ thì $A,B$ trùng nhau nên $m=0,-2$