Cho hình chữ nhật ABCD . Kẻ AH vuông góc với BD
â. Chứng minh tam giác ADH~tam giác DCB và \(BC^2=DH.DB\)
b. Gọi M là trung điểm của BH , N là trung điểm của AH . Chứng minh ΔHMN~ΔHBA
c. Chứng minh : MH.BD= MN.ĐC
đ. Gọi E là trung điểm của DC . Chứng minh AM vuong goc voi ME

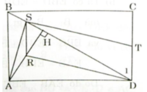
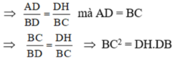
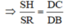
a, xét tam giác ADH và tam giác DBC có:
góc AHD=góc BCD=90 độ
góc ADH= góc DBC (so le trong)
=> tam giác ADH~tam giác DBC
=> AD/DB=DH/BC
mà AD=BC (ABCD là hcn)
=> BC/DB=DH/BC
=> BC.BC=DH.DB
hay \(BC^2\)= DH.DB
b, xét tam giác HAB có:
AN=HN (N là trung điểm của AH)
HM=BM (M là trung đểm của HB)
=> MN là đg tb của tam giác HAB
=> MN//AB
=> tam giác HMN~ tam giác HBA
c, xét tam giác HBA và tam giác CDB có:
góc AHB=góc BCD=90 độ
góc ABH=góc BDC (so le trong)
=> tam giác HBA~tam giác CDB
mà tam giác HBA~tam giác HMN (theo b)
=> tam giác HMN~tam giác CDB
=> HM/CD=MN/BD
=> HM.BD=MN.CD
mình biết làm 3 phần thôi ạ