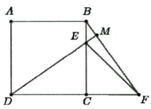
cho hình vuông ABCD cạnh a, M là 1 điểm trên cạnh AB . gọi E là giao của của tia CM và DA. trên tia đối của tia BA lấy điểm F sao cho BF = DE. gọi N là trung điểm của đoạn EF.
xác định vị trí của M để S(ACFE) = 6S(ABCD)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu hỏi của Vũ Huy Hiệu - Toán lớp 9 - Học toán với OnlineMath
Em tham khảobài tương tự tại đây nhé.

a/ \(\widehat{DCE}+\widehat{ECF}=180^o\)
=> \(\widehat{ECF}=90^o\)
Xét t/g DEC và t/g BFC có
EC = FC (GT)
\(\widehat{DCE}=\widehat{BCF}=90^o\)
DC = BC (do ABCD là hình vuông)
=> t/g DEC = t/g BFC (c.g.c)
=> DE = BF (2 cạnh t/ứ(
b/ Xét t/g BEH và t/g DEC có
\(\widehat{BEH}=\widehat{DEC}\) (đối đỉnh)
\(\widehat{EBF}=\widehat{EDC}\) (do t/g BFC = t/g DEC)
\(\Rightarrow\Delta BEH\sim\Delta DEC\) (g.g)
=> \(\widehat{BHE}=\widehat{DCB}=90^o\)
=> \(DE\perp BF\)
Xét t/g BDF có
DE ⊥ BF
BC ⊥ DF
DE cắt BC tại E
=> E là trực tâm t/g BDF
=> .... đpcm
c/ Xét t/g CEF có CE = CF ; M là trung điểm EF
=> CM ⊥ EF
=> \(\widehat{KMC}=90^o\)
Tự cm OKMC làhcn
=> OC = KM => AO = KM
Mà AO // KM (cùng vuông góc vs BD)
=> AOMK là hbh
=> OM // AK

Chứng minh được:
C B F ^ + B E M ^ = M D F ^ + D E C ^ = 90 0
=> B M D ^ = 90 0 nên M thuộc đường tròn đường kính BD. Mà E Î BC nên quỹ tích của điểm M là là cung B C ⏜ của đường tròn đường kính BD

Mk chỉ nêu cách làm bạn tự triển khai nha!
CM \(\Delta ADC=\Delta CBE (g.c.g)\) (*)
(\(\angle C_1=\angle C_2\) cùng phụ với \(\angle ACB\))
\(\Rightarrow AC=CE\Rightarrow \Delta ACE \) cân tại C
\(\Rightarrow AB=CE\)
Từ (*) suy ra:
\(S_{ANEC}=S_{ACE}+S_{ANE}=S_{ABCD}+S_{ANE}\)
\(=\dfrac{1}{2}AB^2+\dfrac{1}{2}NA.2AB=\dfrac{1}{2}AB(AB+2NA)\)
Mà \( S_{ANCE}=\dfrac{15}{8} S_{ABCD}\) \(\Rightarrow \dfrac{15}{8}.\dfrac{1}{2} AB^2=\dfrac{1}{2}.AB(2AN+AB)\)
\(\Rightarrow 2AN+AB=\dfrac{15}{8}AB\) \(\Rightarrow \dfrac{NA}{AB}=\dfrac{7}{16}\)
CM \(\Delta NAM \) đồng dạng với \(\Delta CBM\) \((g.g)\)
\(\Rightarrow \dfrac{NA}{AB}=\dfrac{NA}{BC}=\dfrac{AM}{MB}=\dfrac{7}{16}\)
Vậy cần lấy M sao cho \(\dfrac{AM}{MB}=\dfrac{7}{16}\)