cho (P) y=2x2 và (d) y= -x+3
a) Vẽ (P) và (d) trên cùng một mặt phẳng
c) Cho (D') y +4x -2m =0 .Tìm m để (D') và (P) không có điểm chug
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
28 tháng 2 2021
b) Phương trình hoành độ giao điểm là:
\(-2x^2=x-3\)
\(\Leftrightarrow-2x^2-x+3=0\)
\(\Leftrightarrow-2x^2+2x-3x+3=0\)
\(\Leftrightarrow-2x\left(x-1\right)-3\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(-2x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\-2x-3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\-2x=3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-\dfrac{3}{2}\end{matrix}\right.\)
Thay x=1 vào hàm số y=x-3, ta được:
y=1-3=-2
Thay \(x=-\dfrac{3}{2}\) vào hàm số y=x-3, ta được:
\(x=-\dfrac{3}{2}-3=-\dfrac{9}{2}\)
Vậy: M(1;-2) và \(N\left(-\dfrac{3}{2};-\dfrac{9}{2}\right)\)
12 tháng 5 2023
b: PTHĐGĐ là:
-1/2x^2=1/2x-1
=>-x^2=x-2
=>-x^2-x+2=0
=>x^2+x-2=0
=>x=-2 hoặc x=1
=>y=-1/2*4=-2 hoặc y=-1/2
a: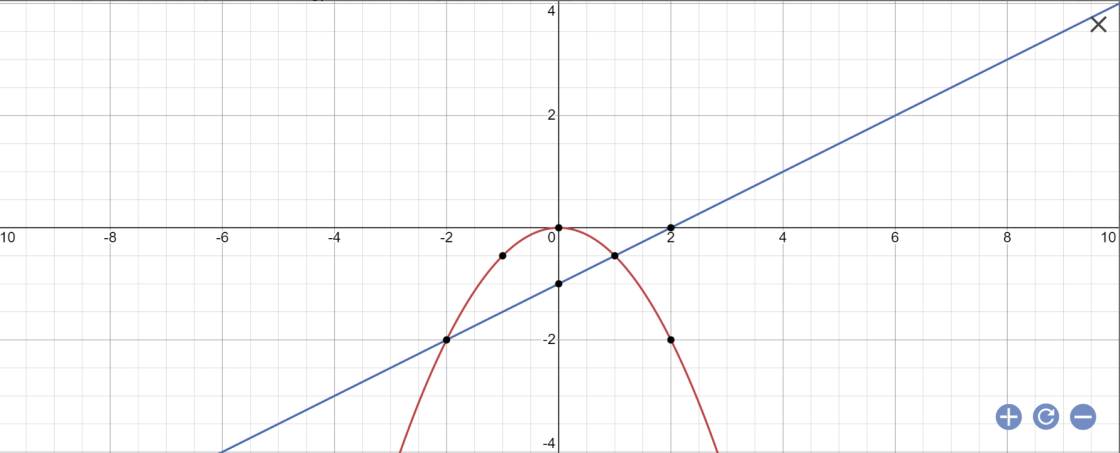 
NA
Nguyễn An Ninh
VIP
12 tháng 5 2023
b. ta có phương trình hoành độ: 1/2.x^2=3/2.x-1 <=>1/2.x^2-3/2.x+1=0 <=> x^2-3x+2=0
Δ=1>0 =>pt có hai nghiệm phân biệt
x=2 =>y=2 =>A (2;2)
x=1 =>y=1/2 =>B(1;1/2)
Vậy (P)và (d) cắt nhau tại hai điểm A(2;2) và B(1;1/2)
19 tháng 11 2021
b. PT hoành độ giao điểm \(x-3=2x+1\Leftrightarrow x=-4\Leftrightarrow y=-7\Leftrightarrow M\left(-4;-7\right)\)
19 tháng 11 2021
Giúp mình vẽ hình với làm nốt mấy câu còn lại nữa
Mình cảm ơn
27 tháng 2 2023
a: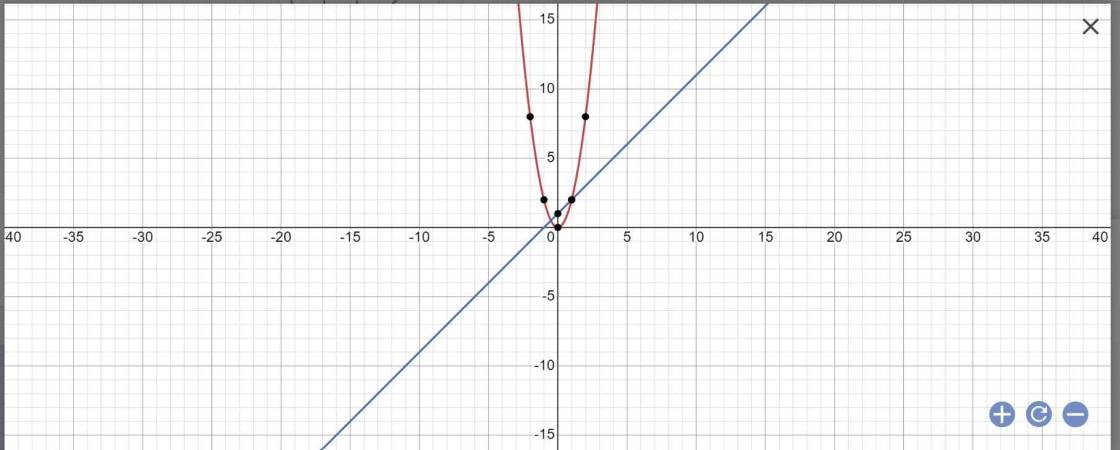 
b: PTHĐGĐ là:
2x^2=x+1
=>2x^2-x-1=0
=>2x^2-2x+x-1=0
=>(X-1)(2x+1)=0
=>x=-1/2 hoặc x=1
=>y=2*1/4=1/2 hoặc y=2
30 tháng 5 2021
a)Tự vẽ
b) Xét pt hoành độ gđ của (P) và (d) có:
\(\dfrac{3}{2}x^2=x+\dfrac{1}{2}\)
\(\Leftrightarrow3x^2-2x-1=0\) \(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{3}\Rightarrow y=\dfrac{3}{2}.\left(-\dfrac{1}{3}\right)^2=\dfrac{1}{6}\\x=1\Rightarrow y=\dfrac{3}{2}\end{matrix}\right.\)
Vậy gđ của (d) và (P) là \(\left(-\dfrac{1}{3};\dfrac{1}{6}\right),\left(1;\dfrac{3}{2}\right)\)
c) Gọi đt cần tìm có dạng (d') \(y=ax+b\) (a2+b2>0)
Gọi A(-4;y1) và B(2;y2) là hai giao điểm của (P) và (d')
\(A;B\in\left(P\right)\Rightarrow\left\{{}\begin{matrix}y_1=24\\y_2=6\end{matrix}\right.\)
\(\Rightarrow A\left(-4;24\right),B\left(2;6\right)\) \(\in\left(d'\right)\)
\(\Rightarrow\left\{{}\begin{matrix}24=-4a+b\\6=2a+b\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}a=-3\\b=12\end{matrix}\right.\) (thỏa)
Vậy (d'): y=-3x+12
Y
21 tháng 3 2023
\(a,\) Tự vẽ nha
\(b,\) Gọi \(A\left(x_A;y_A\right)\) ; \(B\left(x_B;y_B\right)\) là tọa độ giao điểm của (P) và (D)
Ta có :
\(-x^2=x-2\)
\(\Leftrightarrow-x^2-x+2=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_1=1\\x_2=-2\end{matrix}\right.\)
Thay \(x_1=1\) vào (p) : \(y=-x^2\Rightarrow y=-1^2=-1\)
Thay \(x_2=-2\) vào (d) : \(y=x-2\Rightarrow y=-2-2=-4\)
Vậy tọa độ của 2 đồ thị hs là : \(A\left(1;-1\right);B\left(-2;-4\right)\)
c:
y+4x-2m=0
=>y=-4x+2m
Phương trình hoành độ giao điểm là:
\(2x^2=-4x+2m\)
\(\Leftrightarrow x^2+2x-m=0\)
\(\text{Δ}=2^2-4\cdot1\cdot\left(-m\right)=4m+4\)
Để (D') và (P) không có điểm chung là 4m+4<0
hay m<-1