
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a)

b) Phương trình hoành độ giao điểm của hai đường thẳng đã cho:
-3x + 5 = 2x
⇔ 2x + 3x = 5
⇔ 5x = 5
⇔ x = 1 ⇒ y = 2.1 = 2
Vậy M(1; 2)

b: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}3x^2-2x-1=0\\y=3x^2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x^2-3x+x-1=0\\y=3x^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(x-1\right)\left(3x+1\right)=0\\y=3x^2\end{matrix}\right.\Leftrightarrow\left(x,y\right)\in\left\{\left(1;3\right);\left(-\dfrac{1}{3};\dfrac{1}{3}\right)\right\}\)

\(b,\text{PT hoành độ giao điểm: }2x+5=-x+2\Leftrightarrow3x=-3\\ \Leftrightarrow x=-1\Leftrightarrow y=3\Leftrightarrow A\left(-1;3\right)\\ c,\text{PT 2 đt giao Ox: }\left\{{}\begin{matrix}y=0\Rightarrow x=-\dfrac{5}{2}\Rightarrow B\left(-\dfrac{5}{2};0\right)\\y=0\Rightarrow x=2\Rightarrow C\left(2;0\right)\end{matrix}\right.\\ \Rightarrow BC=OB+OC=\dfrac{5}{2}+2=\dfrac{9}{2}\\ \text{Gọi H là chân đường cao từ A tới BC}\\ \Rightarrow AH=\left|y_A\right|=3\\ \Rightarrow S_{ABC}=\dfrac{1}{2}AH\cdot BC=\dfrac{1}{2}\cdot3\cdot\dfrac{9}{2}=\dfrac{27}{4}\left(đvdt\right)\)

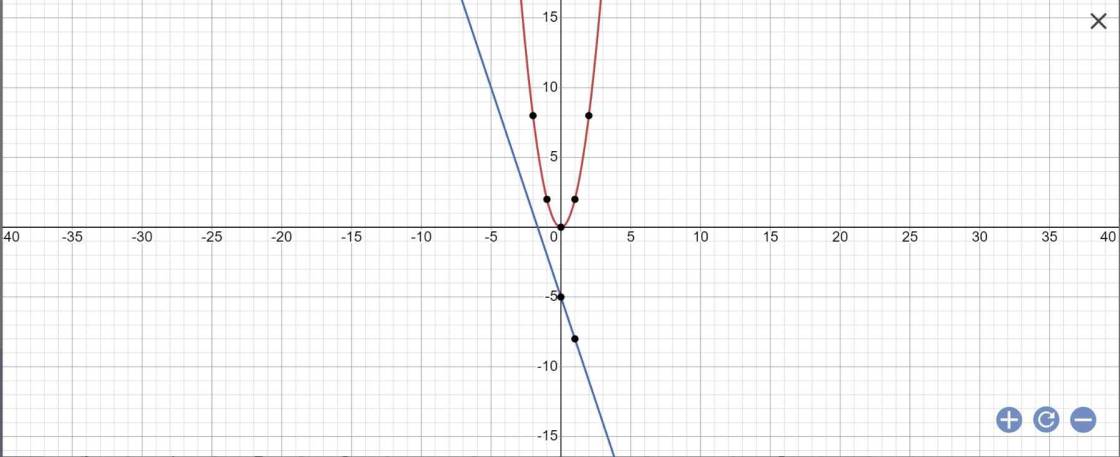
a: 
b: PTHĐGĐ là:
2x^2+3x+1=0
=>x=-1 hoặc x=-1/2
=>y=2 hoặc y=1/2
\(a,\) Tự vẽ nha
\(b,\) Gọi \(A\left(x_A;y_A\right);B\left(x_B;y_B\right)\) là tọa độ của \(\left(P\right)\) và \(\left(d\right)\)
Ta có : \(\left(P\right)=\left(d\right)\)
Suy ra :
\(2x^2=-3x-1\)
\(\Leftrightarrow2x^2+3x+1=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_1=-\dfrac{1}{2}\\x_2=-1\end{matrix}\right.\)
Thay \(x_1=-\dfrac{1}{2}\) vào \(\left(P\right):y=2x^2\Rightarrow y=2.\left(-\dfrac{1}{2}\right)^2=\dfrac{1}{2}\)
Thay \(x_2=-1\) vào \(\left(d\right):y=-3x-1\Rightarrow y=-3.\left(-1\right)-1=2\)
Vậy tọa độ của 2 đồ thị hàm số là \(A\left(-\dfrac{1}{2};\dfrac{1}{2}\right);B\left(-1;2\right)\)

\(a,\) Tự vẽ nhaa
\(b,\) Gọi \(A\left(x_A;y_A\right);B\left(x_B;y_B\right)\) là tọa độ giao điểm của \(\left(P\right)\) và \(\left(d\right)\)
Ta có : \(\left(P\right)=\left(d\right)\)
Suy ra :
\(2x^2=-3x+1\)
\(\Leftrightarrow2x^2+3x-1=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_1=\dfrac{-3+\sqrt{17}}{4}\\x_2=\dfrac{-3-\sqrt{17}}{4}\end{matrix}\right.\)
Thay \(x_1=\dfrac{-3+\sqrt{17}}{4}\) vào \(\left(P\right):y=2x^2\Rightarrow y=2.\left(\dfrac{-3+\sqrt{17}}{4}\right)=\dfrac{-3+\sqrt{17}}{2}\)
Thay \(x_2=\dfrac{-3-\sqrt{17}}{4}\) vào \(\left(d\right):y=-3x+1\Rightarrow y=-3.\left(\dfrac{-3-\sqrt{17}}{4}\right)+1=\dfrac{13+3\sqrt{17}}{4}\)
Vậy toa độ giao điểm của 2 đồ thị hàm số là
\(A\left(\dfrac{-3+\sqrt{17}}{4};\dfrac{-3+\sqrt{17}}{2}\right)\) và \(B\left(\dfrac{-3-\sqrt{17}}{4};\dfrac{13+3\sqrt{17}}{4}\right)\)

b: Tọa độ C là:
5-3x=1/3x+2 và y=5-3x
=>-10/3x=-3 và y=5-3x
=>x=-3:(-10/3)=9/10 và y=5-3*9/10=5-27/10=23/10

b. PTHDGD: \(2x=x+1\Leftrightarrow x=1\Leftrightarrow y=2\Leftrightarrow A\left(1;2\right)\)
Vậy tọa độ giao điểm 2 đt là \(A\left(1;2\right)\)