tính (a-b)^2011bieets a+b=9 và ab=20 và a<b
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Lời giải:
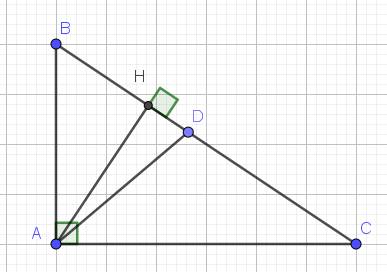
a. Áp dụng định lý Pitago:
$BC=\sqrt{AB^2+AC^2}=\sqrt{12^2+16^2}=20$ (cm)
Áp dụng tính chất đường phân giác:
$\frac{BD}{DC}=\frac{AB}{AC}=\frac{12}{16}=\frac{3}{4}$
Mà: $BD+DC=BC=20$ nên:
$BD=20:(3+4).3=\frac{60}{7}$ (cm)
$CD= 20:(3+4).4=\frac{80}{7}$ (cm)
b.
$AH=2S_{ABC}:BC=\frac{AB.AC}{BC}=\frac{12.16}{20}=9,6$ (cm)
$BH=\sqrt{AB^2-AH^2}=\sqrt{12^2-9,6^2}=7,2$ (cm)
$HD = BD-BH = \frac{60}{7}-7,2=\frac{48}{35}$ (cm)
$AD = \sqrt{AH^2+HD^2}=\sqrt{9,6^2+(\frac{48}{35})^2}=\frac{48\sqrt{2}}{7}$ (cm)

C nằm giữa A và B => AC + BC = AB
D là trung điểm của AC => CD = AC/2
E là trung điểm của BC => CE = BC/2
Vì \(D\in AC;E\in BC\) => C nằm giữa D và E
=> DE = DC + CE = AC/2 + BC/2 = (AC + BC)/2 = AB/2
Vậy DE = a/2
ta có \(DE=DC+CE=\frac{AC}{2}+\frac{CB}{2}=\frac{AC+CB}{2}=\frac{AB}{2}=\frac{a}{2}\left(cm\right)\)

a) Vì △ABC cân tại A
\(\Rightarrow\widehat{ABC}=\widehat{ACB}\)
\(\Rightarrow\frac{1}{2}\widehat{ABC}=\frac{1}{2}\widehat{ACB}\)
\(\Rightarrow\widehat{ABD}=\widehat{ACE}\)
Xét △ABD và △ACE có :
AB = AC (gt)
\(\widehat{A}\)chung (gt)
\(\widehat{ABD}=\widehat{ACE}\) (cmt)
\(\Rightarrow\)△ABD = △ACE (g.c.g)
\(\Rightarrow\)AD = AE (Cặp cạnh tương ứng)
Mà AB = AC
\(\Rightarrow\frac{AE}{AB}=\frac{AD}{AC}\)
\(\Rightarrow\)DE // BC (Định lí Ta-lét)
b) Ta có : ED // BC
\(\Rightarrow\widehat{EDB}=\widehat{DBC}\)(so le trong)
\(\Rightarrow\widehat{EDB}=\widehat{EBD}\)
\(\Rightarrow\)△EBD cân tại E
\(\Rightarrow\)EB = ED
\(\Rightarrow\)EB = 10
Xét △ABC có : DE // BC
\(\Rightarrow\frac{AE}{AB}=\frac{DE}{BC}\)(Định lí Ta-lét đảo)
\(\Rightarrow\frac{AB-EB}{AB}=\frac{DE}{BC}\)
\(\Rightarrow\frac{AB-EB}{AB}=\frac{10}{16}\)
\(\Rightarrow\frac{AB-10}{AB}=\frac{5}{8}\)
\(\Rightarrow5AB=8AB-80\)
\(\Rightarrow AB=\frac{80}{3}\)
Vậy \(AB=\frac{80}{3}\)(đvdt)

Ta có: a/b * b/c = a/c
Từ kết luận trên, tỉ số giữa a và c là: 5/9 * 27/32 = 15/32
Đáp số: 15/32