Tính( không làm tắt cho mình dễ hiểu với ạ)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
7 tháng 9 2021
\(\left(a-\dfrac{a^2+b^2}{a+b}\right)\left(\dfrac{1}{b}+\dfrac{2}{a-b}\right)\)
\(=\dfrac{a^2+ab-a^2-b^2}{a+b}\cdot\dfrac{a-b+2b}{b\left(a-b\right)}\)
\(=\dfrac{b\left(a-b\right)}{a+b}\cdot\dfrac{a+b}{b\left(a-b\right)}\)
=1
TT
2
3 tháng 11 2021
\(a,ĐK:-3x\ge0\Leftrightarrow x\le0\left(-3< 0\right)\\ b,ĐK:4-2x\ge0\Leftrightarrow-2x\ge-4\Leftrightarrow x\le2\\ c,ĐK:\dfrac{1}{2x-5}\ge0\Leftrightarrow2x-5>0\left(1>0;2x-5\ne0\right)\\ \Leftrightarrow x>\dfrac{5}{2}\\ d,ĐK:\dfrac{4x+7}{-3}\ge0\Leftrightarrow4x+7\le0\left(-3< 0\right)\Leftrightarrow x\le-\dfrac{7}{4}\)
NA
1
12 tháng 10 2021
a: \(\sqrt{252}+\dfrac{1}{3}\sqrt{63}-\sqrt{175}\)
\(=4\sqrt{7}+\sqrt{7}-5\sqrt{7}\)
=0
8 tháng 3 2017
\(A=\frac{5}{2.1}+\frac{4}{1.11}+\frac{3}{11.2}+\frac{1}{2.15}+\frac{13}{15.4}\)
\(=\frac{1}{7}\left(\frac{5}{2.7}+\frac{4}{7.11}+\frac{3}{11.14}+\frac{1}{14.15}+\frac{13}{15.28}\right)\)
\(=\frac{1}{7}\left(\frac{1}{2}-\frac{1}{7}+\frac{1}{7}-\frac{1}{11}+\frac{1}{11}-\frac{1}{14}+\frac{1}{14}-\frac{1}{15}+\frac{1}{15}-\frac{1}{28}\right)\)
\(=\frac{1}{2}\left(\frac{1}{2}-\frac{1}{28}\right)\)
\(=\frac{1}{2}.\frac{13}{28}\)
\(=\frac{13}{56}\)
17 tháng 2 2022
unpollute
deforestation
environmental
pollution
conservationists
prevention
extremely
environmentalist
protection
seriously
poisonous
UH
1
19 tháng 6 2016
txđ D=R
y'=-3x2+6x+3m
y' là tam thức bậc 2 nên y'=0 có tối đa 2 nghiệm
để hs nb/(0;\(+\infty\) ) thì y' \(\le\) 0 với mọi x \(\in\) (0;\(+\infty\) )
\(\Leftrightarrow\) -3x2 +6x+3m \(\le\) 0 với mọi x \(\in\) (0;\(+\infty\) )
\(\Leftrightarrow\) m\(\le\) x2 -2x với mọi x \(\in\) (0; \(+\infty\) )
xét hs g(x)=x2 -2x
g'(X) =2x-2
g'(x)=0 \(\Leftrightarrow\) x=1
vậy m \(\le\) -1
SV
Sinh Viên NEU
CTVVIP
22 tháng 11 2023
Mình dịch theo cả câu nhé : chuyến đi đến Phong Nha Kẻ Bàng là một trải nghiệm khó quên
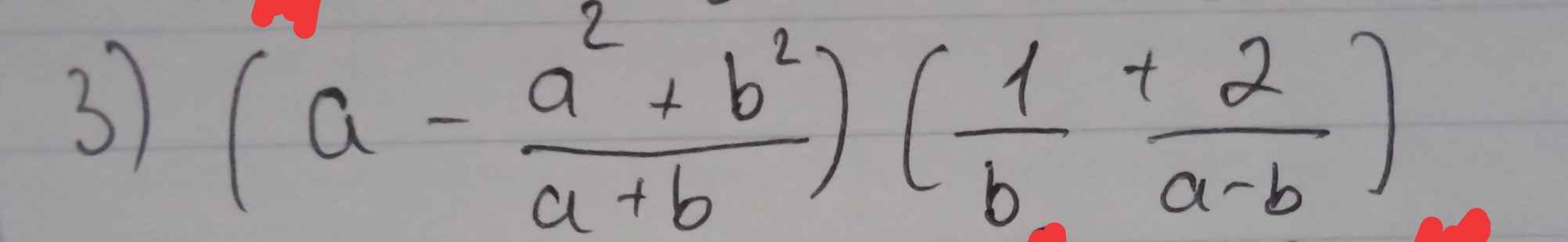
\(\left(a-\dfrac{x^2+a^2}{x+a}\right)\left(\dfrac{2a}{x}-\dfrac{4a}{x-a}\right)\)
\(=\dfrac{ax+a^2-x^2-a^2}{x+a}\cdot\dfrac{2ax-2a^2-4ax}{x\left(x-a\right)}\)
\(=\dfrac{a\left(x-a\right)}{x+a}\cdot\dfrac{-2a^2-2ax}{x\left(x-a\right)}\)
\(=\dfrac{a}{x+a}\cdot\dfrac{-2a\left(a+x\right)}{x}\)
\(=\dfrac{-2a^2}{x}\)
\(\left(a-\dfrac{x^2+a^2}{x+a}\right)\left(\dfrac{2a}{x}-\dfrac{4a}{x-a}\right)\)
\(=\dfrac{ax+a^2-x^2-a^2}{x+a}.\dfrac{2a\left(x-a\right)-4ax}{x\left(x-a\right)}\)
\(=\dfrac{x\left(a-x\right)}{x+a}.\dfrac{-2a^2-2ax}{x\left(x-a\right)}\)
\(=\dfrac{x\left(a-x\right)}{x+a}.\dfrac{-2a\left(a+x\right)}{x\left(x-a\right)}\)
\(=2a\)