Cho tam giác ABC . Tìm điểm M sao cho →MA 2→MB 3→MC →0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


38.
Gọi I là trung điểm AB và G là trọng tâm tam giác ABC
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{MA}+\overrightarrow{MB}=2\overrightarrow{MI}\\\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}\end{matrix}\right.\)
\(3\left|\overrightarrow{MA}+\overrightarrow{MB}\right|=2\left|\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\right|\)
\(\Leftrightarrow3.\left|2\overrightarrow{MI}\right|=3\left|\overrightarrow{MG}+\overrightarrow{GA}+\overrightarrow{MG}+\overrightarrow{GB}+\overrightarrow{MG}+\overrightarrow{GC}\right|\)
\(\Leftrightarrow6\left|\overrightarrow{MI}\right|=2.\left|3\overrightarrow{MG}\right|\)
\(\Leftrightarrow6\left|\overrightarrow{MI}\right|=6\left|\overrightarrow{MG}\right|\)
\(\Leftrightarrow\left|\overrightarrow{MI}\right|=\left|\overrightarrow{MG}\right|\)
\(\Leftrightarrow MI=MG\)
\(\Rightarrow\) Tập hợp M là đường trung trực của đoạn thẳng IG

\(\Leftrightarrow\overrightarrow{MA}\left(\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\right)=\overrightarrow{0}\)
=>vecto MA=0 hoặc M là trọng tâm của ΔABC
=>M là trọng tâm của ΔABC hoặc M trùng với A

Em tham khảo nhé!
Câu hỏi của channel Anhthư - Toán lớp 7 - Học toán với OnlineMath

a: \(\overrightarrow{MA}-\overrightarrow{MB}+\overrightarrow{MC}=\overrightarrow{0}\)
=>\(\overrightarrow{BM}+\overrightarrow{MA}+\overrightarrow{MC}=\overrightarrow{0}\)
=>\(\overrightarrow{BA}+\overrightarrow{MC}=\overrightarrow{0}\)
=>\(\overrightarrow{BA}=\overrightarrow{CM}\)
=>BAMC là hình bình hành
=>M là điểm thỏa mãn BAMC là hình bình hành
Gọi K là trung điểm của BC
\(2\overrightarrow{NA}+\overrightarrow{NB}+\overrightarrow{NC}=\overrightarrow{0}\)
=>\(2\overrightarrow{NA}+2\overrightarrow{NK}=\overrightarrow{0}\)
=>\(\overrightarrow{NA}+\overrightarrow{NK}=\overrightarrow{0}\)
=>N là trung điểm của AK

Ta thấy \(\overrightarrow{MA}-\overrightarrow{MB}+\overrightarrow{MC}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{MA}+\overrightarrow{BM}+\overrightarrow{MC}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{BA}=\overrightarrow{CM}\)
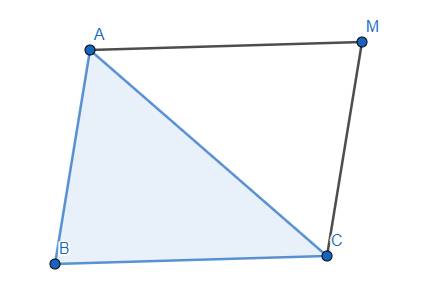
Như vậy, điểm M chính là đỉnh thứ tư của hình bình hành ABCM.

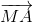 +
+ = 2
= 2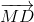
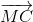 =
= 
\(\overrightarrow{MA}+2\overrightarrow{MB}+3\overrightarrow{MC}=\overrightarrow{0}\)
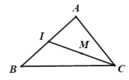
Gọi I, J lần lượt là trung điểm của BC,AC.
K là trọng tâm của tam giác JBC ta có:
(−−→MB+−−→MC)(−−→MA+2−−→MB+3−−→MC)=0
⇔2−−→MI.[(−−→MA+−−→MC)+2−−→MB+2−−→MC]=0
⇔2−−→MI.(2−−→MJ+2−−→MB+2−−→MC)=0
⇔4−−→MI(−−→MJ+−−→MB+−−→MC)=0
⇔4−−→MI.3−−−→MK=0
⇔12−−→MI.−−−→MK=0
⇔−−→MI.−−−→MK=0
⇒MI⊥MK⇒ˆIMK=900
Do đó điểm M luôn nhìn đoạn IK một góc 90 độ hay tập hợp điểm M cần tìm là đường tròn đường kính IK