Giải phương trình
6x^4 + 5x^3 - 38x^2 + 5x + 6 = 0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
21 tháng 8 2017
f ) \(\left(x+1\right)\left(x+2\right)\left(x+3\right)\left(x+4\right)-24\)
\(=\left[\left(x+1\right)\left(x+4\right)\right]\left[\left(x+2\right)\left(x+3\right)\right]-24\)
\(=\left(x^2+5x+4\right)\left(x^2+5x+6\right)-24\)
Đặt \(x^2+5x+5=t\), ta có :
\(\left(t-1\right)\left(t+1\right)-24\)
\(=t^2-1-24=t^2-25\)
\(=\left(t-5\right)\left(t+5\right)\)
Thay và ta có :
\(\left(x^2+5x+5-5\right)\left(x^2+5x+5+5\right)\)
\(=\left(x^2+5x\right)\left(x^2+5x+10\right)\)
\(=x\left(x+5\right)\left(x^2+5x+10\right)\)
CM
23 tháng 12 2019
5x3 – x2 – 5x + 1 = 0
⇔ x2(5x – 1) – (5x – 1) = 0
⇔ (x2 – 1)(5x – 1) = 0
⇔ (x – 1)(x + 1)(5x – 1) = 0
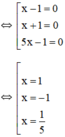
Vậy phương trình có tập nghiệm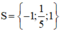 
PT
1
CM
18 tháng 7 2019
a) 1,2x3 – x2 – 0,2x = 0
⇔ 0,2x.(6x2 – 5x – 1) = 0
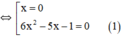
Giải (1): 6x2 – 5x – 1 = 0
có a = 6; b = -5; c = -1
⇒ a + b + c = 0
⇒ (1) có hai nghiệm x1 = 1 và x2 = c/a = -1/6.
Vậy phương trình ban đầu có tập nghiệm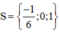 
b) 5x3 – x2 – 5x + 1 = 0
⇔ x2(5x – 1) – (5x – 1) = 0
⇔ (x2 – 1)(5x – 1) = 0
⇔ (x – 1)(x + 1)(5x – 1) = 0
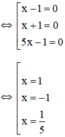
Vậy phương trình có tập nghiệm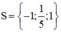 
MT
2
CW
27 tháng 8 2017
pt bậc 4 => có 4 nghiệm.
bấm máy tính tìm nghiệm đẹp (-2 và 3). Chia sơ đồ hoocne.
2 nghiệm đẹp (-2 và 3) được rồi, còn 2 nghiệm còn lại thì giải pt bậc 2 là ra.
kq: x=-2, x=3, x=1/3 , x=-1/2
23 tháng 11 2018
Ta có \(6x^4-5x^3-38x^2-5x+6=0\Leftrightarrow6x^4+12x^3-17x^3-34x^2-4x^2-8x+3x+6=0\Leftrightarrow6x^3\left(x+2\right)-17x^2\left(x+2\right)-4x\left(x+2\right)+3\left(x+2\right)=0\Leftrightarrow\left(x+2\right)\left(6x^3-17x^2-4x+3\right)=0\Leftrightarrow\left(x+2\right)\left(6x^3-18x^2+x^2-3x-x+3\right)=0\Leftrightarrow\left(x+2\right)\left[6x^2\left(x-3\right)+x\left(x-3\right)-\left(x-3\right)\right]=0\Leftrightarrow\left(x+2\right)\left(x-3\right)\left(6x^2+x-1\right)=0\Leftrightarrow\left(x+2\right)\left(x-3\right)\left(6x^2-2x+3x-1\right)=0\Leftrightarrow\left(x+2\right)\left(x-3\right)\left[2x\left(3x-1\right)+\left(3x-1\right)\right]=0\Leftrightarrow\left(x+2\right)\left(x-3\right)\left(3x-1\right)\left(2x+1\right)=0\Leftrightarrow\)\(\left[{}\begin{matrix}x+2=0\\x-3=0\\3x-1=0\\2x+1=0\end{matrix}\right.\)\(\Leftrightarrow\)\(\left[{}\begin{matrix}x=-2\\x=3\\x=\dfrac{1}{3}\\x=-\dfrac{1}{2}\end{matrix}\right.\)
Vậy S={\(-\dfrac{1}{2};-2;\dfrac{1}{3};3\)}
15 tháng 10 2015
Giúp tôi giải toán - Hỏi đáp, thảo luận về toán học - Học toán với OnlineMath tích mình nha
LH
1
12 tháng 8 2021
1: Ta có: \(x^2+7x+6=0\)
\(\Leftrightarrow\left(x+1\right)\left(x+6\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=-6\end{matrix}\right.\)
2: Ta có: \(x^2+7x+12=0\)
\(\Leftrightarrow\left(x+3\right)\left(x+4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=-4\end{matrix}\right.\)
3: Ta có: \(x^2+8x+15=0\)
\(\Leftrightarrow\left(x+3\right)\left(x+5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=-5\end{matrix}\right.\)
4: Ta có: \(x^2+5x+4=0\)
\(\Leftrightarrow\left(x+1\right)\left(x+4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=-4\end{matrix}\right.\)
22 tháng 7 2021
b) 5x(x-2000)-x+2000=0
\(\Rightarrow5x\left(x-2000\right)-\left(x-2000\right)=0\\ \Rightarrow\left(x-2000\right)\left(5x-1\right)=0\)
\(\Rightarrow\left\{{}\begin{matrix}x-2000=0\\5x-1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0+2000\\5x=0+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2000\\5x=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2000\\x=\dfrac{1}{5}\end{matrix}\right.\)
\(6x^4+5x^3-38x^2+5x+6=0\\ \Leftrightarrow6x^4+20x^3+6x^2-15x^3-50x^2-15x+6x^2+20x+6=0\\ \Leftrightarrow2x^2\left(3x^2+10x+3\right)-5x\left(3x^2+10x+3\right)+2\left(3x^2+10x+3\right)=0\\ \Leftrightarrow\left(3x^2+10x+3\right)\left(2x^2-5x+2\right)=0\\ \Leftrightarrow\left(3x^2+x+9x+3\right)\left(2x^2-x-4x+2\right)=0\\ \Leftrightarrow\left[x\left(3x+1\right)+3\left(3x+1\right)\right]\left[x\left(2x-1\right)-2\left(2x-1\right)\right]=0\\ \Leftrightarrow\left(3x+1\right)\left(x+3\right)\left(2x-1\right)\left(x-2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}3x+1=0\\x+3=0\\2x-1=0\\x-2=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{-1}{3}\\x=-3\\x=\dfrac{1}{2}\\x=2\end{matrix}\right.\)