Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, biết AB=a , AD =a√3. Hình chiếu S lên đáy là trung điểm H lên AB, góc tạo bởi SD và đáy là 60 độ . Thể tích của khối chóp S.ABCD là bao nhiêu?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án A
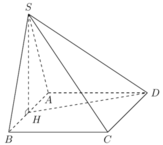
Ta có tam giác AHD vuông tại A, suy ra
H D = A H 2 + D H 2 = a 2 4 + a 2 = a 5 2
Tam giác SHD vuông tại H, suy ra:
S
H
=
S
D
2
-
H
D
2
=
13
a
2
4
-
5
a
2
4
=
a
2
Vậy V S . A B C D = a 3 2 3

Đáp án A
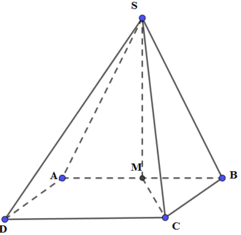
Phương pháp:
+) Xác định góc giữa SC và mặt đáy là góc giữa SC và hình chiếu của nó trên (ABCD).
+) Áp dụng định lí Pytago tính SM.
![]()
Cách giải:
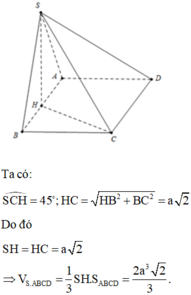
Gọi M là trung điểm của AB ⇒ SM ⊥ (ABCD)


Đáp án C
Ta có: Xét ∆ A D H vuông tại A có:
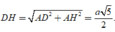
Xét ∆ S D H vuông tại H có:
![]()
S H K D C = 5 S A B C D 8 = 5 a 2 8 (đvdt)
⇒ V S . H K D C = 1 3 . 5 a 2 8 . a 3 = 5 a 3 3 24 (đvtt)

Đáp ván A
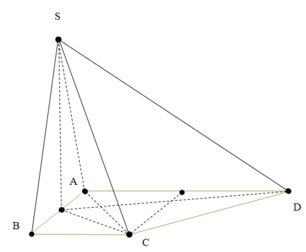
Vì I là hình chiếu của S trên (ABCD)
⇒ ( S C → , ( A B C D ) ) = S C I ⏞
⇒ S I = I C . tan 60 ° = a 5 2 . tan 60 ° = a 15 2
Vậy
V S . I B C = V S . A B C D - V S . A I B - V S . I C D = 1 3 . a 15 2 a + 2 a 2 . a - 1 2 . a 2 . 2 a - 1 2 . a 2 . a = a 3 15 8
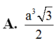

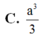
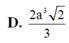
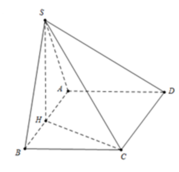
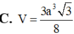
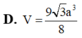
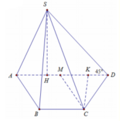


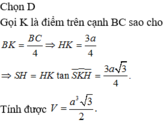
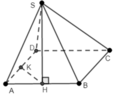

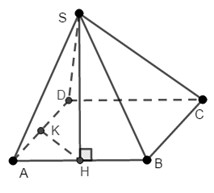
\(AH=HB=\dfrac{a}{2}\).
\(DH=\sqrt{\left(a\sqrt{3}\right)^2+\left(\dfrac{a}{2}\right)^2}=\dfrac{\sqrt{13}a}{2}\).
\(SH=DH.tan\widehat{SDH}=\dfrac{\sqrt{13}a}{2}.tan60^o=\dfrac{\sqrt{39}a}{2}\).
Thể tích khối chóp S.ABCD là: \(\dfrac{1}{3}.SH.S_{ABCD}=\dfrac{1}{3}.\dfrac{\sqrt{39}a}{2}.a.\sqrt{3}a=\dfrac{\sqrt{13}a^3}{2}\).