Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
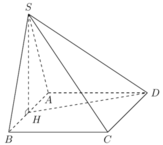
Ta có tam giác AHD vuông tại A, suy ra
H D = A H 2 + D H 2 = a 2 4 + a 2 = a 5 2
Tam giác SHD vuông tại H, suy ra:
S
H
=
S
D
2
-
H
D
2
=
13
a
2
4
-
5
a
2
4
=
a
2
Vậy V S . A B C D = a 3 2 3

Đáp án A
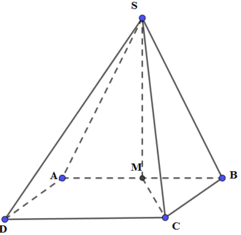
Phương pháp:
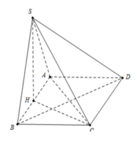
+) Xác định góc giữa SC và mặt đáy là góc giữa SC và hình chiếu của nó trên (ABCD).
+) Áp dụng định lí Pytago tính SM.
![]()
Cách giải:
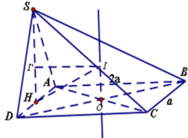
Gọi M là trung điểm của AB ⇒ SM ⊥ (ABCD)


Đáp án C
Ta có: Xét ∆ A D H vuông tại A có:
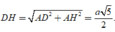
Xét ∆ S D H vuông tại H có:
![]()
S H K D C = 5 S A B C D 8 = 5 a 2 8 (đvdt)
⇒ V S . H K D C = 1 3 . 5 a 2 8 . a 3 = 5 a 3 3 24 (đvtt)
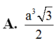

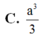
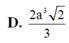
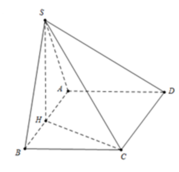
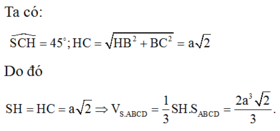
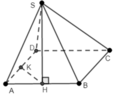

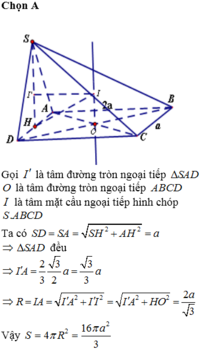
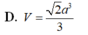
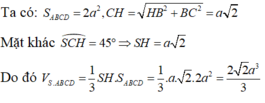
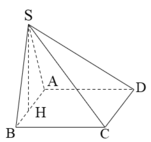
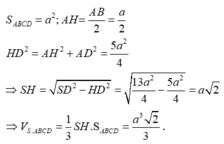
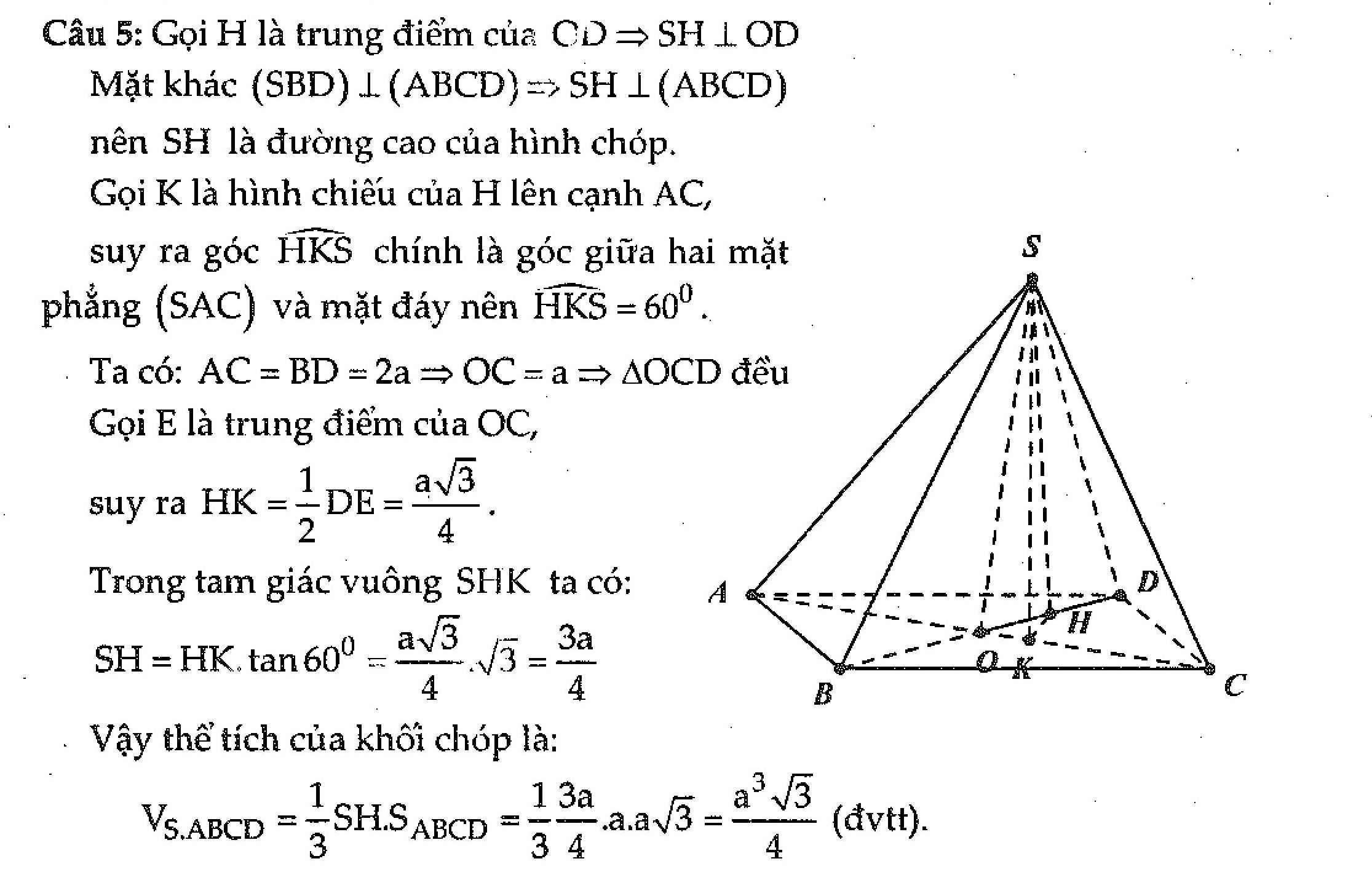
\(AH=HB=\dfrac{a}{2}\).
\(DH=\sqrt{\left(a\sqrt{3}\right)^2+\left(\dfrac{a}{2}\right)^2}=\dfrac{\sqrt{13}a}{2}\).
\(SH=DH.tan\widehat{SDH}=\dfrac{\sqrt{13}a}{2}.tan60^o=\dfrac{\sqrt{39}a}{2}\).
Thể tích khối chóp S.ABCD là: \(\dfrac{1}{3}.SH.S_{ABCD}=\dfrac{1}{3}.\dfrac{\sqrt{39}a}{2}.a.\sqrt{3}a=\dfrac{\sqrt{13}a^3}{2}\).