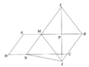
Cho hình bình hành ABCD. Lấy trên cạnh AB, CD các đường thẳng bằng nhau AE=CF , lấy trên AD và BC các đường thẳng bằng nhau AM=CN . Chứng minh : Tứ giác EMFN là hình bình hành ; Gọi I là giao điểm của AC và BD , Chứng minh : EF và MN cùng đi qua điểm I
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) - Xét \(\Delta AME\) và \(\Delta CNF\) có :
+ AM = CN (GT)
+ \(\widehat{MAE}=\widehat{NCF}\)(GT)
+ AE = CF ( GT )
=> \(\Delta AME=\Delta CNF\left(c.g.c\right)\) => ME = NF ( 2 cạnh tương ứng bằng nhau )
- Tương tự , \(\Delta DMF=\Delta BNE\left(c.g.c\right)\) => MF = NE ( 2 cạnh tương ứng bằng nhau )
- Xét tứ giác EMFN có :
+ ME = NF
+ MF = NE
=> EMFN là hình bình hành ( 2 cặp cạnh đối bằng nhau )
b) Vì ABCD là Hình bình hành => AC cắt BD tại I => I là trung điểm của AC , BD (1)
Tương tự AC cắt EF và MN tại trung điểm I của AC (2)
Từ 1 và 2 => EF và MN đều đi qua I


Ta có AECF là hình bình hành=> EF cắt AC ở trung điểm I của mỗi đường
AMCN là hình bình hành=>MN cắt AC ở trung điểm của mỗi đường
=>EF cắt MN ở trung điểm mỗi đường=> ĐPCM

Gọi O là giao điểm 2 đường chéo AC và BD
Xét \(\Delta\)AOE và \(\Delta\)COF có:AO=OC ( vì ABCD là hình bình hành ),CF=AE ( giả thiết ),^AOE=^COF ( đối đỉnh )
a
Vì vậy \(\Delta AOE=\Delta COF\left(c.g.c\right)\Rightarrow OE=OF\left(1\right)\)
Xét \(\Delta\)BON và \(\Delta\)DOM có:OB=OD ( vì ABCD là hình bình hành ),MD=BN ( vì AM=CN ),^MOD=^NOB ( đối đỉnh )
Vì vậy \(\Delta BON=\Delta COM\left(c.g.c\right)\Rightarrow OM=ON\left(2\right)\)
Từ \(\left(1\right);\left(2\right)\) suy ra tứ giác EMFN là hình bình hành.
b
Hình bình hành EMFN có O là giao điểm của 2 đường chéo,tứ giác ABCD có O là giao điểm của 2 đường chéo.
=> ĐPCM
P/S:Mik ko chắc lắm đâu nha,nhất là câu b ý:p

a: Ta có: AE+EB=AB
CF+FD=CD
mà AB=CD
và AE=CF
nên EB=FD
Ta có: AM+MD=AD
CN+NB=CB
mà AD=CB
và AM=CN
nên MD=NB
Xét ΔAME và ΔCNF có
AM=CN
\(\widehat{A}=\widehat{C}\)
AE=CF
Do đó: ΔAME=ΔCNF
Suy ra: ME=NF
Xét ΔEBN và ΔFDM có
BE=DF
\(\widehat{B}=\widehat{D}\)
BN=DM
Do đó: ΔEBN=ΔFDM
Suy ra: EN=FM
Xét tứ giác EMFN có
EN=MF
EM=NF
Do đó: EMFN là hình bình hành

a.Xét ΔAME và ΔCNF có
AM=CN(gt)
Góc MAE= góc NCF
AE=CF(gt)
Do đó ΔAME = ΔCNF (c.g.c)
=> ME=NF(2 cạnh tương ứng)
Tương tự ΔDMF= ΔBNE(c.g.c)
=>MF=NE(2 cạnh tương ứng)
Tứ giác EMFN có
ME=NF(gt)
MF=NE(gt)
=>EMFN là hình bình hành
b) b/ Ta có: OE=OF (MENF là hình bình hành)
ON=OM(MENF là hình bình hành)
OD=OB (ABCD là hình bình hành)
OA=OC(ABCDlà hình bình hành)
=>AC, BD, MN, E giao nhau tại O
hay AC, BD, MN, EF đồng quy
cn lại bó tay

a) Do AM = DN Þ MADN là hình bình hành
⇒ D ^ = A M N ^ = E M B ^ = M B C ^
Ta có DMPE = DBPE nên EP = FP. Vậy MEBF là hình thoi và 2 điểm E, F đối xứng nhau qua AB.
b) Tứ giác MEBF có MB Ç EF = P; Lại có P trung điểm BM, P là trung điểm EF, MB ^ EF.
Þ MEBF là hình thoi.
c) Để BNCE là hình thang cân thì C N E ^ = B E N ^
Mà
C N E ^ = D ^ = M B C ^ = E B M ^ nên DMEB có 3 góc bằng nhau, suy ra điều kiện để BNCE là hình thang cân thì A B C ^ = 60 0
+ Xét \(\Delta AEM\) và \(\Delta CFN\) ,có :
\(AE=CF\) ( gt )
\(AM=CN\left(gt\right)\)
\(\widehat{EAM}=\widehat{FCN}\)( \(ABCD\) là hbh )
\(\Rightarrow\Delta AEM=\Delta CFN\left(cgc\right)\)
\(\Rightarrow EM=FN\)(1)
Ta có :
\(AE+EB=AB;CF+FD=CD\)
Mà \(AE=CF;AB=CD\)
\(\Rightarrow BE=DF\) .C/ m Tương tự ,có : \(DM=BN\)
Ta cũng có : \(\Delta BEN=\Delta DFM\left(cgc\right)\) => MF = EN(2)
Từ (1)(2) => ENFM là hình bình hành
bạn ơi tớ cần ý sau