Tìm tất cả các giá trị thực của tham số m để hàm số y=x3-3mx2-9m2x nghịch biến trên khoảng (0;1)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án A
Phương pháp: Để hàm số nghịch biến trên ![]() và y’ = 0 tại hữu hạn điểm.
và y’ = 0 tại hữu hạn điểm.
Cách giải: TXĐ: D =R
![]()
![]()
![]()
![]()
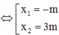
![]() nằm trong khoảng 2 nghiệm x1; x2
nằm trong khoảng 2 nghiệm x1; x2
Hàm số nghịch biến trên khoảng (0;1) khi và chỉ khi:
TH1: 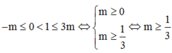
TH2: 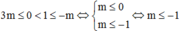
Vậy m ≥ 1 3 hoặc m ≤ - 1

Đáp án C.
Ta có:
y ' = 3 x 2 − 6 m x − 9 m 2 = 3 x 2 − 2 m x − 3 m 2 = 3 x + m x − 3 m
TH1: Nếu m > 0 ⇒ y ' < 0 ⇔ − m < x < 3 m nên hàm số nghịch biến trên 0 ; 1 ⇒ 3 m > 1 − m < 0 ⇔ m > 1 3 .
TH2: Nếu m < 0 ⇒ y ' < 0 ⇔ 3 m < x < − m nên hàm số nghịch biến trên 0 ; 1 ⇒ − m > 1 3 m < 0 ⇔ m < − 1.
TH3: Nếu m = 0 ⇒ y ' = 3 x 2 ≥ 0 ∀ x ∈ 0 ; 1 nên hàm số đồng biến trên ℝ

Đáp án B
Xét hàm số f x = 1 π x 3 − 3 m x 2 + m , ta có f ' x = 3 x 2 − 6 m x . 1 π x 3 − 3 m x 2 + m . ln 1 π .
Để hàm số đã cho nghịch biến trên khoảng
− ∞ ; + ∞ ⇔ f ' x ≤ 0 ; ∀ x ∈ ℝ ⇔ 3 x 2 − 6 m x ≥ 0 ; ∀ x ∈ ℝ
⇔ x x − 2 m ≥ 0 ; ∀ x ∈ ℝ ⇒ m = 0 là giá trị cần tìm.

Đáp án B
Xét hàm số f x = 1 π x 3 - 3 m x 2 + m , ta có
f ' x = 3 x 2 - 6 m x . 1 π x 3 - 3 m x 2 + m . ln 1 π .
Để hàm số đã cho nghịch biến trên khoảng - ∞ ; + ∞
⇔ f ' x ≤ 0 ; ∀ x ∈ ℝ ⇔ 3 x 2 - 6 m x ≥ 0 ; ∀ x ∈ ℝ
⇔ x x - 2 m ≥ 0 ; ∀ x ∈ ℝ ⇒ m = 0 .

Đáp án B
Phương pháp:
Hàm số y = f(x) nghịch biến trên (-∞;+∞) khi và chỉ khi f'(x) ≤ 0, ∀ x ∈ (-∞;+∞), f'(x) = 0 tại hữu hạn điểm.
Cách giải:
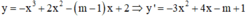
Hàm số đã cho nghịch biến trên khoảng (-∞;+∞)
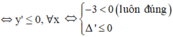
![]()
![]()
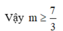
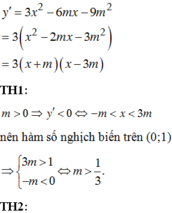
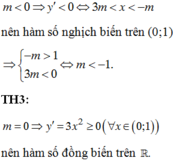


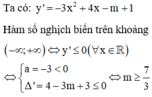
\(TXĐ:D=R\)
\(y=x^{3}-3mx^{2}-9m^{2}x\)
\(y'=3x^{2}-6mx-9m^{2}=0\)
\(\Leftrightarrow\)\(y'=3(x+m)(x-3m)=0\)
\(\left[\begin{array}{} x=-m\\ x=3m \end{array} \right.\)
\(y'<0\) \(\forall\)\(x\) \(\in\)\((0,1)\).Ta xét các trường hợp
\(TH1:-m\)\(\le\)\(0\)\(<1\)\(\le\)\(3m\)
\(\Leftrightarrow\)\(m \)\(\ge\)\(\dfrac{1}{3}\)
\(TH2:3m\)\(\le\)\(0\)<\(1\)\(\le\)\(-m\)
\(\Leftrightarrow\)\(m\)\(\le\)\(-1\)
Vậy \(m\)\(\ge\)\(\dfrac{1}{3}\) hoặc \(m\)\(\le\)\(-1\)
\(\Leftrightarrow\)\(m \)\(\ge\)\(\dfrac{1}{3}\)
cái tương đương dưới cùng là sai nha.Nó bị nhảy