Phân tích đa thức thành nhân tử:
a) x2 +5x = 6
b) x2 - 2015.x + 2014 = 0
Giuso mk vs đúng mk tíkA
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Cách 1: Tách một hạng tử thành tổng hai hạng tử để xuất hiện nhân tử chung.
a) x2 – 3x + 2
= x2 – x – 2x + 2 (Tách –3x = – x – 2x)
= (x2 – x) – (2x – 2)
= x(x – 1) – 2(x – 1) (Có x – 1 là nhân tử chung)
= (x – 1)(x – 2)
Hoặc: x2 – 3x + 2
= x2 – 3x – 4 + 6 (Tách 2 = – 4 + 6)
= x2 – 4 – 3x + 6
= (x2 – 22) – 3(x – 2)
= (x – 2)(x + 2) – 3.(x – 2) (Xuất hiện nhân tử chung x – 2)
= (x – 2)(x + 2 – 3) = (x – 2)(x – 1)
b) x2 + x – 6
= x2 + 3x – 2x – 6 (Tách x = 3x – 2x)
= x(x + 3) – 2(x + 3) (có x + 3 là nhân tử chung)
= (x + 3)(x – 2)
c) x2 + 5x + 6 (Tách 5x = 2x + 3x)
= x2 + 2x + 3x + 6
= x(x + 2) + 3(x + 2) (Có x + 2 là nhân tử chung)
= (x + 2)(x + 3)
Cách 2: Đưa về hằng đẳng thức (1) hoặc (2)
a) x2 – 3x + 2
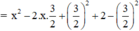
(Vì có x2 và 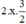 nên ta thêm bớt
nên ta thêm bớt 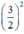 để xuất hiện HĐT)
để xuất hiện HĐT)
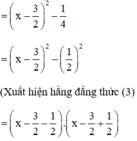
= (x – 2)(x – 1)
b) x2 + x - 6

= (x – 2)(x + 3).
c) x2 + 5x + 6

= (x + 2)(x + 3).

* Chứng minh:
Phương trình a x 2 + b x + c = 0 có hai nghiệm x 1 ; x 2
⇒ Theo định lý Vi-et: 
Khi đó : a.(x – x1).(x – x2)
= a.(x2 – x1.x – x2.x + x1.x2)
= a.x2 – a.x.(x1 + x2) + a.x1.x2
= 
= a . x 2 + b x + c ( đ p c m ) .
* Áp dụng:
a) 2 x 2 – 5 x + 3 = 0
Có a = 2; b = -5; c = 3
⇒ a + b + c = 2 – 5 + 3 = 0
⇒ Phương trình có hai nghiệm 
Vậy: 
b) 3 x 2 + 8 x + 2 = 0
Có a = 3; b' = 4; c = 2
⇒ Δ ’ = 4 2 – 2 . 3 = 10 > 0
⇒ Phương trình có hai nghiệm phân biệt:


`@` `\text {Ans}`
`\downarrow`
`a)`
`6x^2 - 3xy`
`= 3x(2x - y)`
`b)`
Bạn ghi lại đầy đủ thông tin
`c)`
`x^2 - 5x + 6`
`= x^2 - 2x - 3x +6`
`= (x^2 - 2x) - (3x - 6)`
`= x(x - 2) - 3(x - 2)`
`= (x - 3)(x - 2)`
a: =3x*2x-3x*y
=3x(2x-y)
c: =x^2-2x-3x+6
=x(x-2)-3(x-2)
=(x-2)(x-3)
b: Bạn ghi đầy đủ đề nha bạn

* Chứng minh:
Phương trình ax2 + bx + c = 0 có hai nghiệm x1; x2
⇒ Theo định lý Vi-et: 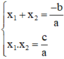
Khi đó : a.(x – x1).(x – x2)
= a.(x2 – x1.x – x2.x + x1.x2)
= a.x2 – a.x.(x1 + x2) + a.x1.x2
= 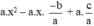
= a.x2 + bx + c (đpcm).
* Áp dụng:
a) 2x2 – 5x + 3 = 0
Có a = 2; b = -5; c = 3
⇒ a + b + c = 2 – 5 + 3 = 0
⇒ Phương trình có hai nghiệm 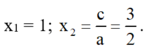
Vậy: 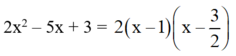

a) (x - 2)(x - 3). b) 3(x - 2)(x + 5).
c) (x - 2)(3x + 1). d) (x-2y)(x - 5y).
e) (x + l)(x + 2)(x - 3). g) (x-1)(x + 3)( x 2 + 3).
h) (x + y - 3)(x - y + 1).

a: \(x^2-6x+5=\left(x-5\right)\left(x-1\right)\)
b: \(x^2-x-12=\left(x-4\right)\left(x+3\right)\)
c: \(x^2+8x+15=\left(x+5\right)\left(x+3\right)\)
d: \(2x^2-5x-12=\left(x-4\right)\left(2x+3\right)\)
e: \(x^2-13x+36=\left(x-9\right)\left(x-4\right)\)
Giải:
a) \(x^2+5x=6\)
\(\Leftrightarrow x^2+5x-6=0\)
\(\Leftrightarrow x^2+6x-x-6=0\)
\(\Leftrightarrow\left(x^2+6x\right)-\left(x+6\right)=0\)
\(\Leftrightarrow x\left(x+6\right)-\left(x+6\right)=0\)
\(\Leftrightarrow\left(x+6\right)\left(x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+6=0\\x-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-6\\x=1\end{matrix}\right.\)
Vậy ...
b) \(x^2-2015x+2014=0\)
\(\Leftrightarrow x^2-2014x-x+2014=0\)
\(\Leftrightarrow\left(x^2-2014x\right)-\left(x-2014\right)=0\)
\(\Leftrightarrow x\left(x-2014\right)-\left(x-2014\right)=0\)
\(\Leftrightarrow\left(x-2014\right)\left(x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-2014=0\\x-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2014\\x=1\end{matrix}\right.\)
Vậy ...
Chúc bạn học tốt!
\(a,x^2+5x=6\)
\(\Rightarrow x^2+5x-6=0\)
\(\Rightarrow x^2+6x-x-6=0\)
\(\Rightarrow\left(x^2-6x\right)-\left(x+6\right)=0\)
\(\Rightarrow x\left(x+6\right)-\left(x+6\right)=0\)
\(\Rightarrow\left(x+6\right)\left(x-1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x+6=0\\x-1=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=-6\\x=1\end{matrix}\right.\)
\(b,x^2+2015x+2014=0\)
\(\Rightarrow x^2+2015x+2015-1=0\)
\(\Rightarrow\left(x^2-1\right)+\left(2015x+2015\right)=0\)
\(\Rightarrow\left(x-1\right)\left(x+1\right)+2015\left(x+1\right)=0\)
\(\Rightarrow\left(x+1\right)\left(x-1+2015\right)=0\)
\(\Rightarrow\left(x+1\right)\left(x+2014\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x+1=0\\x+2014=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=-1\\x=-2014\end{matrix}\right.\)