Bài 3. Cho đường tròn (O,R), đường kính AB. Từ điểm M bất kỳ trên đường tròn vẽ tiếp tuyến cắt 2 tiếp tuyến tại A, B lần lượt tại C và D. a) Chứng minh CD = CA + DB. b/ Chứng minh 𝐶𝑂𝐷 ̂ = 900 . c) Chứng minh AC . BD = R2 . d) Cho 𝑀𝐴𝐵 ̂ = 600 . CM : BDM đều, tính cạnh và S BDM theo R. Bài 4. Cho đường tròn (O,R), M ở ngoài đường tròn sao cho OM=2R. Vẽ tiếp tuyến MA của (O) với A là tiếp điểm. a) OAM là tam giác gì ? Tính cạnh và góc OMA ? b) Kẻ tiếp tuyến MB của (O). Chứng minh OM ⊥ AB. c) Vẽ cát tuyến MEF với đường tròn (O) (E nằm giữa M,F). Gọi I là trung điểm của EF. Chứng minh 5 điểm A, O, I, B, M cùng thuộc một đường tròn. Bài 5. Từ điểm A ở ngoài (O,R) với OA = 2R, vẽ 2 tiếp tuyến AB và AC. a) Chứng minh OA là trung trực của BC. b) Tính AB, AC theo R. c) Chứng minh ABC đều. Tính S ABC . d) Từ 1 điểm M thuộc 𝐵𝐶⏜ nhỏ kẻ tiếp tuyến thứ 3 cắt 2 tiếp tuyến kia tại P và Q. Chứng minh chu vi APQ có giá trị không đổi khi M thuộc 𝐵𝐶⏜ nhỏ.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét (O) có
CA là tiếp tuyến có A là tiếp điểm
CM là tiếp tuyến có M là tiếp điểm
Do đó: CA=CM
Xét (O) có
DM là tiếp tuyến có M là tiếp điểm
DB là tiếp tuyến có B là tiếp điểm
Do đó: DM=DB
Ta có: CD=CM+MD
nên CD=CA+DB

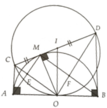
a, Dễ thấy A M B ^ = 90 0 hay E M F ^ = 90 0 tiếp tuyến CM,CA
=> OC ⊥ AM => O E M ^ = 90 0 Tương tự => O F M ^ = 90 0
Chứng minh được ∆CAO = ∆CMO => A O C ^ = M O C ^
=> OC là tia phân giác của A M O ^
Tương tự OD là tia phân giác của B O M ^ suy ra OC ⊥ OD <=> C O D ^
b, Do ∆AOM cân tại O nên OE là đường phân giác đồng thời là đường cao
=> O E M ^ = 90 0 chứng minh tương tự O F M ^ = 90 0
Vậy MEOF là hình chữ nhật
c, Gọi I là trung điểm CD thì I là tâm đường tròn đường kính CD và IO=IC=ID. Có ABDC là hình thang vuông tại A và B nên IO//AC//BD và IO vuông góc với AB. Do đó AB là tiếp tuyến của đường tròn đường kính CD.

a: Xét (O) có
CM là tiếp tuyến
CA là tiếp tuyến
Do đó: CM=CA và OC là tia phân giác của góc MOA(1)
Xét (O) có
DM là tiếp tuyến
DB là tiếp tuyến
Do đó: DM=DB và OD là tia phân giác của góc MOB(2)
Ta có: CM+DM=CD
nên CD=CA+DB
b: Từ (1) và (2) suy ra \(\widehat{COM}+\widehat{DOM}=\dfrac{1}{2}\left(\widehat{MOA}+\widehat{MOB}\right)=90^0\)
=>\(\widehat{COD}=90^0\)
hay ΔCOD vuông tại O

Sử dụng tính chất hai tiếp tuyến
a, Ta có: AC = CM; BD = DM => AC+BD=CD
b, C O A ^ = C O M ^ ; D O M ^ = D O B ^
=> C O D ^ = 90 0
c, AC.BD = MC.MD = M O 2 = R 2
d, Gọi I là trung điểm của CD. Sử dụng tính chất trung tuyến ứng với cạnh huyền trong tam giác vuông và đường trung bình trong hình thang để suy ra đpcm

bạn tham khảo ở đây nha,mình từng giải rồi
https://hoc24.vn/cau-hoi/cho-duong-tron-o-duong-kinh-ab-tren-tiep-tuyen-tai-a-cua-duong-trong-o-lay-diem-c-ve-tuyep-tuyen-cn-va-cat-tuyen-cde-tia-cd-nam-giua-2-tai-ca-co-de-thuoc-duong-tron-o-d-nam-giua-c-va-e.1081799079177

Xét (O) có
CM,CA là tiếp tuyến
=>CM=CA và OC là phân giác của góc MOA(1)
Xét (O) có
DM,DB là tiếp tuyến
=>DM=DB và OD là phân giác của góc MOB(2)
Từ (1), (2) suy ra góc COD=1/2*góc AOB=90 độ
=>O nằm trên (I)
Xét hình thang ABDC có
O,I lần lượt là trung điểm của AB,CD
=>OI là đường trung bình
=>OI//AC//BD
=>OI vuông góc AB
=>AB tiếp xúc (I) tại O

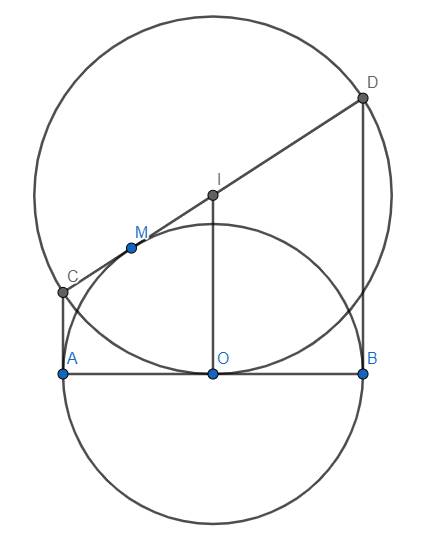
Dễ thấy ABDC là hình thang. Vì O, I lần lượt là trung điểm của AB, CD nên OI là đường trung bình của hình thang ABDC.
\(\Rightarrow\left\{{}\begin{matrix}OI//AC//BD\Rightarrow OI\perp AB\left(tạiO\right)\\OI=\dfrac{AC+BD}{2}=\dfrac{CM+DM}{2}=\dfrac{CD}{2}=R\end{matrix}\right.\) với R là bán kính của đường tròn \(\left(CD\right)\).
Từ đó suy ra AB tiếp xúc (I) tại O. (đpcm)