Đặt điện áp xoay chiều u=\(U_ocos\omega t\) có \(U_o\) không đỏi và \(\omega\) thay đổi được vào hai đầu đoạn mạch R, L, C mắc nối tiếp. Thay đổi \(\omega\) thì cường độ dòng điện hiệu dụng trong mạch khi \(\omega=\omega_1\) bằng cường độ dòng điện hiệu dụng trong mạch khi \(\omega=\omega_2\) . Hiệu thức đúng là:
A. \(\omega_1.\omega_2=\dfrac{1}{\sqrt{LC}}\) B. \(\omega_1+\omega_2=\dfrac{2}{LC}\) C....
Đọc tiếp
Đặt điện áp xoay chiều u=\(U_ocos\omega t\) có \(U_o\) không đỏi và \(\omega\) thay đổi được vào hai đầu đoạn mạch R, L, C mắc nối tiếp. Thay đổi \(\omega\) thì cường độ dòng điện hiệu dụng trong mạch khi \(\omega=\omega_1\) bằng cường độ dòng điện hiệu dụng trong mạch khi \(\omega=\omega_2\) . Hiệu thức đúng là:
A. \(\omega_1.\omega_2=\dfrac{1}{\sqrt{LC}}\) B. \(\omega_1+\omega_2=\dfrac{2}{LC}\) C. \(\omega_1.\omega_2=\dfrac{1}{LC}\) D. \(\omega_1+\omega_2=\dfrac{2}{\sqrt{LC}}\)
Ai giúp mình đi ạ!
có
U
0
không đổi và thay đổi được vào hai đầu đoạn mạch có R, L, C mắc nối tiếp. Thay đổi 
" 
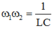
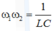
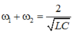
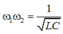
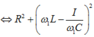
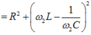
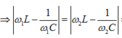
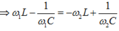
Cường độ dòng hiệu dụng: \(I=\dfrac{U}{Z}\)
Ta có: \(I_1=I_2\)
\(\Rightarrow \dfrac{U}{Z_1}=\dfrac{U}{Z_2}\)
\(\Rightarrow Z_1=Z_2\)
\(\Rightarrow \sqrt{R^2+(Z_{L1}-Z_{C1})^2}=\Rightarrow \sqrt{R^2+(Z_{L2}-Z_{C2})^2}\)
\(\Rightarrow Z_{L1}-Z_{C1}=Z_{C2}-Z_{L2}\)
\(\Rightarrow Z_{L1}+Z_{L2}=Z_{C1}+Z_{C2}\)
\(\Rightarrow \omega_1.L+\omega_2.L=\dfrac{1}{\omega_1C}+\dfrac{1}{\omega_2C}\)
\(\Rightarrow (\omega_1+\omega_2)L=\dfrac{1}{C}.\dfrac{\omega_1+\omega_2}{\omega_1.\omega_2}\)
\(\Rightarrow \omega_1.\omega_2=\dfrac{1}{LC}\)
Chọn C