Thực hiện phép chia: (đơn thức-đa thức)
(-x^4+2x-3x^2) : (x-2)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
C
3
Những câu hỏi liên quan
27 tháng 8 2021
\(\dfrac{-x^4-3x^2+2x}{x-2}\)
\(=\dfrac{-x^4+2x^3-2x^3+4x^2-7x^2+14x-12x+24-24}{x-2}\)
\(=-x^3-2x^2-7x-12+\dfrac{-24}{x-2}\)
C
2
27 tháng 8 2021
\(\dfrac{-x^4-3x^2+2x}{x-2}\)
\(=\dfrac{-x^4+2x^3-2x^3+4x^2-7x^2+14x-12x+24-24}{x-2}\)
\(=-x^3-2x^2-7x-12+\dfrac{-24}{x-2}\)
24 tháng 12 2021
b: \(\dfrac{A\left(x\right)}{B\left(x\right)}=\dfrac{x^4-\dfrac{1}{2}x^3+\dfrac{1}{2}x^3-\dfrac{1}{4}x^2+\dfrac{9}{4}x^2-\dfrac{9}{8}x-\dfrac{15}{8}x+\dfrac{15}{16}+a-\dfrac{1}{16}}{2x-1}\)
Để A(x) chia hết cho B(x) thì a-1/16=0
hay a=1/16
4 tháng 1 2022
a: \(=\dfrac{x\left(x^2+x-2\right)}{x+2}=\dfrac{x\left(x+2\right)\left(x-1\right)}{x+2}=x^2-x\)
b: \(=\dfrac{x^3-3x^2+2x+24}{x+2}=\dfrac{x^3+2x^2-5x^2-10x+12x+24}{x+2}=x^2-5x+12\)
5 tháng 1 2022
\(x^2\left(y-1\right)-4\left(y-1\right)\\ =\left(y-1\right)\left(x^2-4\right)=\left(y-1\right)\left(x-2\right)\left(x+2\right)\)
DT
0
31 tháng 10 2020
Bài 1.
3x2 + 2 có bậc thấp hơn x3 + 1 nên không thể chia tiếp
Vậy x3 + 3x2 + 3 = 1( x3 + 1 ) + 3x2 + 2
Bài 2.
Ta có : x3 + 3x2 + 3x + a có bậc là 3
x + 2 có bậc là 1
=> Thương bậc 2
lại có hệ số cao nhất của đa thức bị chia là 1
Đặt đa thức thương là x2 + bx + c
khi đó : x3 + 3x2 + 3x + a chia hết cho x + 2
<=> x3 + 3x2 + 3x + a = ( x + 2 )( x2 + bx + c )
<=> x3 + 3x2 + 3x + a = x3 + bx2 + cx + 2x2 + 2bx + 2c
<=> x3 + 3x2 + 3x + a = x3 + ( b + 2 )x2 + ( c + 2b )x + 2c
Đồng nhất hệ số ta được :
\(\hept{\begin{cases}b+2=3\\c+2b=3\\2c=a\end{cases}}\Leftrightarrow\hept{\begin{cases}b=1\\c=1\\a=2\end{cases}}\Rightarrow a=2\)
Vậy a = 2
LK
25 tháng 8 2018
a)xy(x2+2y)=xy.x2+xy.2y
=x3y+2xy2
b)-4(6x2-xy)=-4.6x2+4.xy
=-24x2+4xy
c)4x[x2+6x-1/2]
=4x.x2+4x.6x-4x.1/2
=4x3+24x2-2x
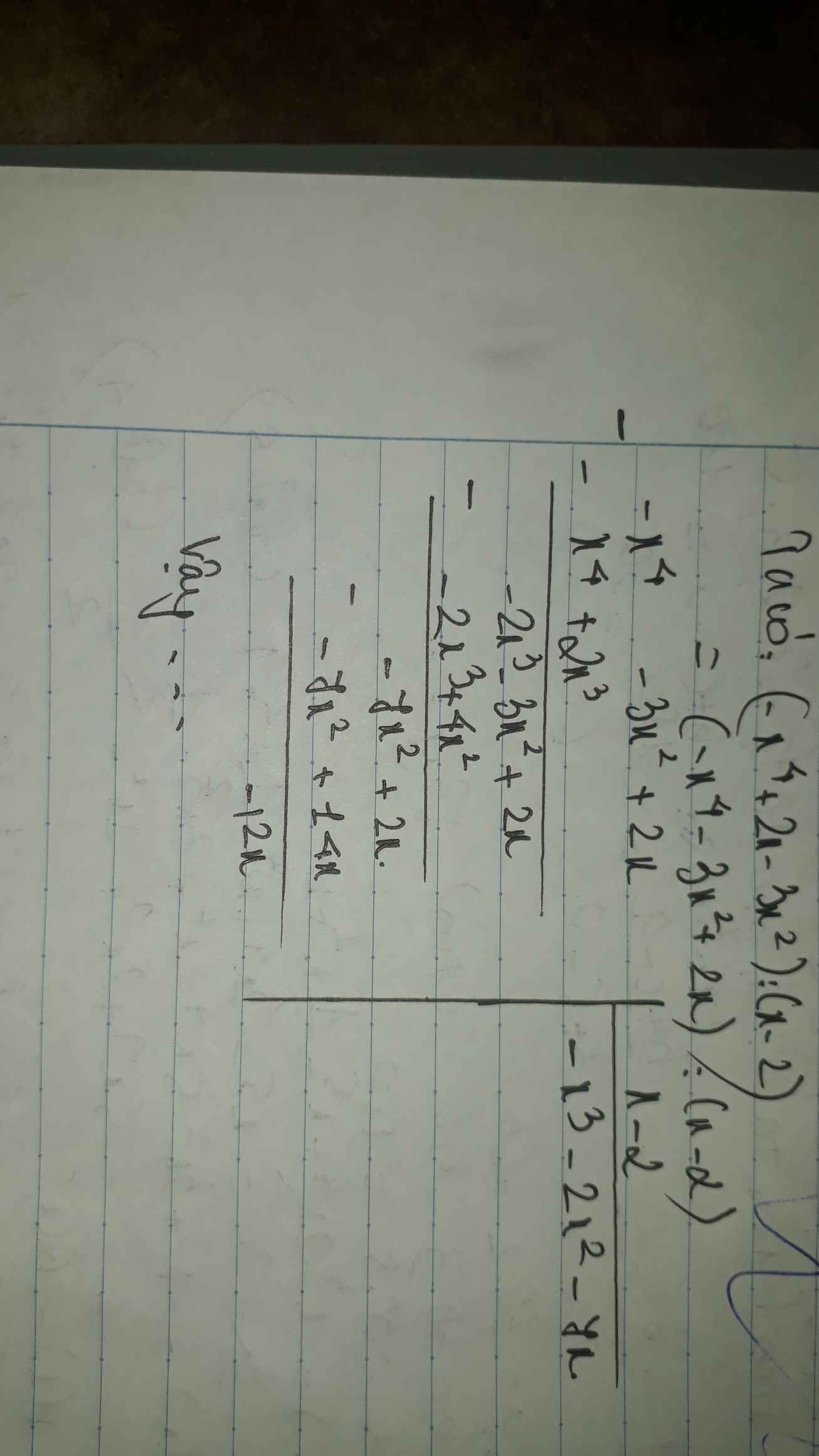
`(-x^4+2x-3x^2):(x-2)`
`=[-x(x^3+3x-2)]:(x-2)`
`=[-x(x^3-2x^2+2x^2-4x+7x-14+12)]:(x-2)`
`={-x[x^2(x-2)+2x(x-2)+7(x-2)]-12x+24-24}:(x-2)`
`=[-x(x-2)(x^2+2x+7)-12(x-2)-24]:(x-2)`
`=-x(x^2+2x+7)-12` và dư `-24`
`=-x^3-2x^2-7x-12` và dư `-24`