cho hình bình hành ABCD, kẻ AM vuông góc với BD tại N. Chứng minh a,AMCN là hình bình hành. b, gọi I là trung điểm của MN chứng minh I là trung điểm của AC Giúp mình với mình đang cần gấp lắm!
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a/ Xét △AMD vuông tại M và △CNB vuông tại N có:
- \(AD=BC\) (ABCD là hình bình hành)
- \(\hat{ADM}=\hat{CBN}\) (AD // BC)
⇒ △AMD = △CNB (c.h-g.n) ⇒ AM=NC (1)
\(\begin{matrix}AM\perp MN\\AN\perp NC\end{matrix}\left(gt\right)\Rightarrow AM\text{ // }NC\left(2\right)\)
Từ (1) và (2). Vậy: AMCN là hình bình hành (đpcm)
============
b/ AC và MN là hai đường chéo của hình bình hành AMNC
- Mà I là trung điểm MN
Vậy: I là trung điểm của AC (Trong hình bình hành, hai đường chéo cắt nhau tại trung điểm của mỗi đường) (đpcm)
Xét ΔADM vuông tại M và ΔCBN vuông tại N có
AD=BC
\(\widehat{ADM}=\widehat{CBN}\)
Do đó: ΔADM=ΔCBN
Suy ra: AM=CN
Xét tứ giác AMCN có
AM//CN
AM=CN
Do đó: AMCN là hình bình hành
Suy ra: Hai đường chéo AC và MN cắt nhau tại trung điểm của mỗi đường
mà I là trung điểm của MN
nên I là trung điểm của AC

a: Xét tứ giác AMCN có
AM//CN
AM=CN
Do đó: AMCN là hình bình hành

a: Xét tứ giác AMCN có
AM//CN
AM=CN
Do đó: AMCN là hình bình hành

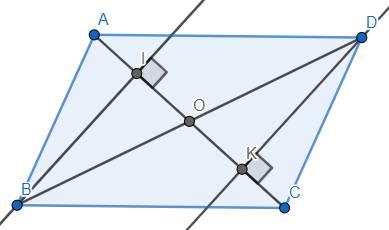
b) Vì BI vuông góc với AC tại I, nên I thuộc AC.
Vì DK vuông góc với AC tại K, nên K thuộc AC.
Vì O là giao điểm của AC và BD nên O thuộc AC.
Suy ra I, O, K là các điểm thuộc AC; từ đó ba điểm I, O, K thẳng hàng

a: Xét ΔAHD vuông tại H và ΔCKB vuông tại K có
AD=CB
góc ADH=góc CBK
=>ΔAHD=ΔCKB
=>AH=CK
mà AH//CK
nên AHCK là hình bình hành
b: AHCK là hình bình hành
=>AC cắt HK tại trung điểm của mỗi đường
=>I là trung điểm của AC
ABCD là hình bình hành
=>AC cắt BD tại trung điểm của mỗi đường
=>I là trung điểm của BD
=>IB=ID

a: Xét tứ giác DEBF có
BE//DF
BE=DF
Do đó: DEBF là hình bình hành
b: ta có: DEBF là hình bình hành
nên Hai đường chéo DB và EF cắt nhau tại trung điểm của mỗi đường(1)
Ta có:ABCD là hình bình hành
nên hai đường chéo AC và BD cắt nhau tại trung điểm của mỗi đường(2)
Từ (1) và (2) suy ra BD,EF,AC đồng quy

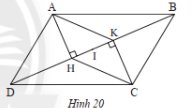
a) Vì \(AH\), \(CK\) vuông góc với \(BD\) (gt)
Suy ra \(AH\) // \(CK\)
Vì \(ABCD\) là hình bình hành (gt)
Suy ra \(AD = BC\); \(AD\) // \(BC\)
Xét \(\Delta ADH\) và \(\Delta CBK\) ta có:
\(\widehat {{\rm{AHD}}} = \widehat {{\rm{CKB}}} = 90^\circ \) (gt)
\(AD = BC\) (cmt)
\(\widehat {{\rm{ADH}}} = \widehat {{\rm{CBK}}}\) (do \(AD\) // \(BC\))
Suy ra \(\Delta ADH = \Delta CBK\) (ch-gn)
Suy ra \(AH = CK\) (hai cạnh tương ứng)
Mà \(AH\) // \(CK\) (cmt)
Suy ra \(AHCK\) là hình bình hành
b) Vì \(AHCK\) là hình bình hành nên hai đường chéo \(HK\) và \(AC\) cắt nhau tại trung điểm.
Mà \(I\) là trung điểm của \(HK\).
Suy ra \(I\) là trung điểm của \(AC\).
Ta lại có \(ABCD\) là hình bình hành nên hai đường chéo \(AC\) và \(BD\) cắt nhau tại trung điểm.
Suy ra \(I\) là trung điểm của \(BD\) hay \( IB = ID\)
a: Xét ΔADM vuông tại M và ΔCBN vuông tại N có
AD=BC
\(\widehat{ADM}=\widehat{CBN}\)
Do đó: ΔADM=ΔCBN
Suy ra: AM=CN
Xét tứ giác AMCN có
AM//CN
AM=CN
Do đó: AMCN là hình bình hành