Bài 31 : Vẽ góc xAy và tia phân giác At . Lấy điểm D trên At . Từ D kẻ đường thẳng vuông góc với At và cắt Ox, Oy lần lượt ở B và C . Chứng minh AB = AC ( nhớ giải đúng và vẽ hình nha )
help me !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
26 tháng 7 2023
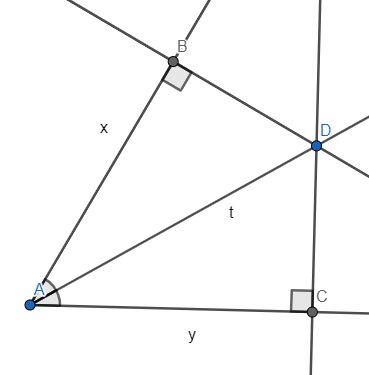
Vì At là tia phân giác của \(\widehat{xAy}\) nên \(\widehat{BAD}=\widehat{CAD}\)
Xét ΔBAD vuông tại B và ΔCAD vuông tại C có:
- AD là cạnh chung
- \(\widehat{BAD}=\widehat{CAD}\) (chứng minh trên)
Suy ra ΔBAD = ΔCAD (cạnh huyền - góc nhọn), từ đó AB = AC (vì hai cạnh tương ứng)
30 tháng 10 2016
Bạn tự vẽ hình nhé !
\(\Delta ADB,\Delta ADC\)có AB = AC ;\(\widehat{BAD}=\widehat{CAD}\)(At là phân giác góc xAy) ; chung AD
\(\Rightarrow\Delta ADC=\Delta ADB\left(c.g.c\right)\)\(\Rightarrow\hept{\begin{cases}DC=DB\\\widehat{ACD}=\widehat{ABD}\end{cases}}\)mà\(\widehat{ABD}=90^0\)(DB _|_ Ax tại B) =>\(\widehat{ACD}=90^0\)=>DC _|_ Ay
Xét \(\Delta ABD\) vuông tại B và \(\Delta ACD\) vuông tại C có:
\(AD\) chung
\(\widehat{BAD}=\widehat{CAD}\) (At là tia pg)
\(\Rightarrow\Delta ABD=\Delta ACD\left(ch-gn\right)\)
\(\Rightarrow AB=AC.\)
ch - gn là j vậy bn ?