\(\Delta\)ABC có 3 góc nhọn . Chứng minh rằng : SABC =\(\dfrac{1}{2}\) b.c.sinA =\(\dfrac{1}{2}\) a.b.sinC=\(\dfrac{1}{2}\) a.c.sinhB
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HP
1 tháng 7 2021
1.
\(sinA+sinB-sinC=2sin\dfrac{A+B}{2}.cos\dfrac{A-B}{2}-sin\left(A+B\right)\)
\(=2sin\dfrac{A+B}{2}.cos\dfrac{A-B}{2}-2sin\dfrac{A+B}{2}.cos\dfrac{A+B}{2}\)
\(=2sin\dfrac{A+B}{2}.\left(cos\dfrac{A-B}{2}-cos\dfrac{A+B}{2}\right)\)
\(=2sin\dfrac{A+B}{2}.2sin\dfrac{A}{2}.sin\dfrac{B}{2}\)
\(=4sin\dfrac{A}{2}.sin\dfrac{B}{2}.cos\dfrac{C}{2}\)
Sao t lại đc như này v, ai check hộ phát
4 tháng 2 2022
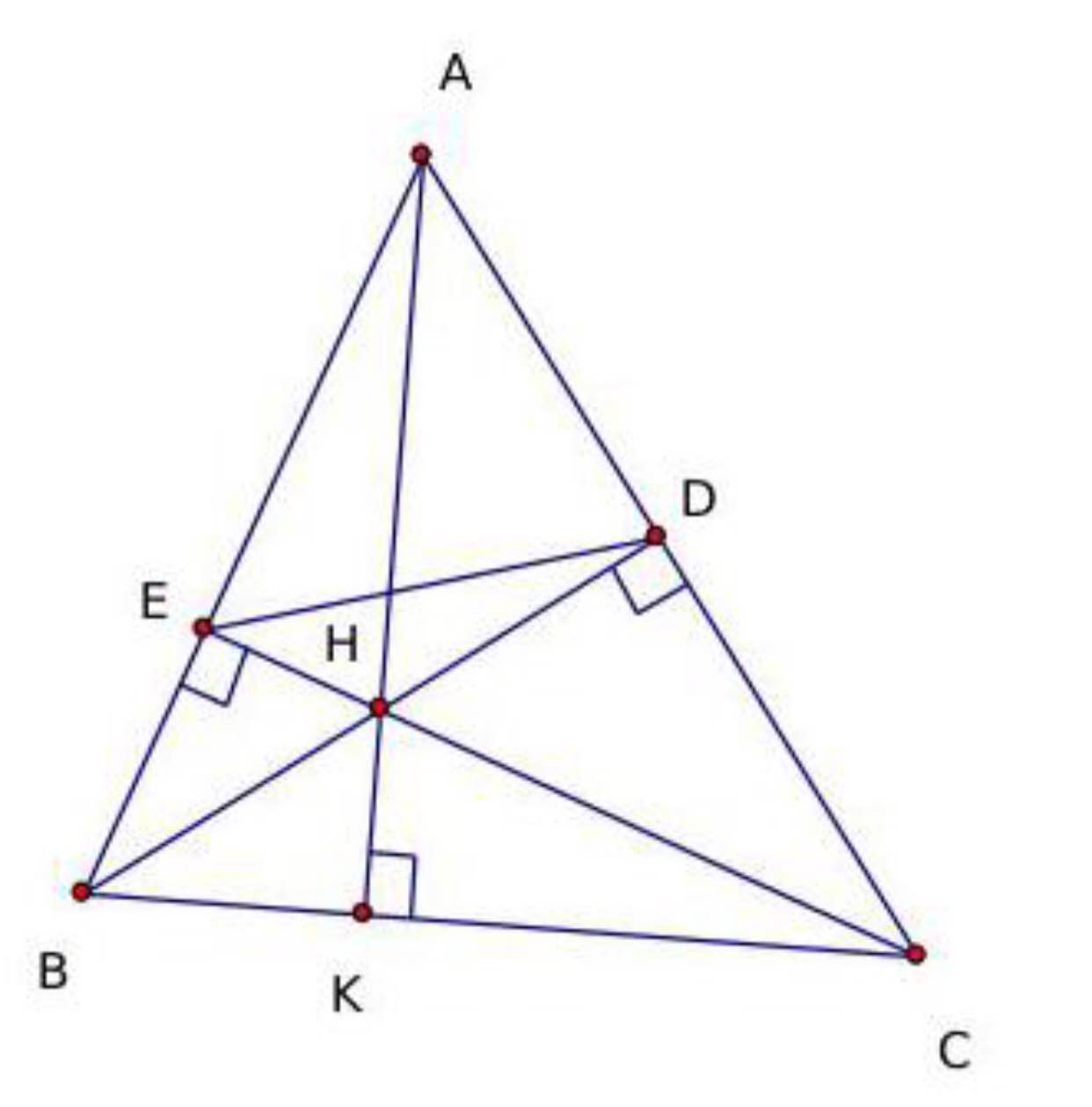
a, Áp dụng định lí Pitago
\(\dfrac{AC^2+CB^2-BA^2}{CB^2+BA^2-AC^2}\\ =\dfrac{AK^2+KC^2+\left(BK+KC\right)^2-AB^2}{\left(BK+KC^2\right)+BA^2-\left(AK+KC\right)^2}\\ =\dfrac{2CK^2+2BK.CK}{2BK^2+2BK.Ck}\\ =\dfrac{2CK\left(CK+BK\right)}{2BK\left(BK+CK\right)}=\dfrac{CK}{BK}\)
b, Ta có
\(tanB=\dfrac{AK}{BK};tanC=\dfrac{AK}{CK}\\ Nên:tanBtanC=\dfrac{AK^2}{BK.CK}\left(1\right)\\ Mặt.khác.ta.có:\\ B=HKC\\ mà:tanHKc=\dfrac{KC}{KH}\\ Nên.tanB=\dfrac{KC}{KH}\\ Tương.tự.tanC=\dfrac{KB}{KH}\\ \Rightarrow tanB.tanC=\dfrac{KB.KC}{KH^2}\left(2\right)\)
Từ (1) và (2)
\(\Rightarrow\left(tanB.tanC\right)^2=\left(\dfrac{AK}{KH}\right)^2\\ Theo.GT:\\ HK=\dfrac{1}{3}AK\Rightarrow tanB.tanC=3\)
c, Chứng minh được
\(\Delta ABC.và.\Delta ADE.đồng.dạng\\ \Rightarrow\dfrac{S_{ABC}}{S_{ADE}}=\left(\dfrac{AB}{AD}\right)^2\left(3\right)\)
Mà
\(\widehat{BAC}=60^0\Rightarrow\widehat{ABD}=30^0\\\Rightarrow AB=2AD\left(4\right)\\ Từ.\left(3\right)và\left(4\right)=4\\ \Rightarrow S_{ADE}=30cm^2\)
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 7 2021
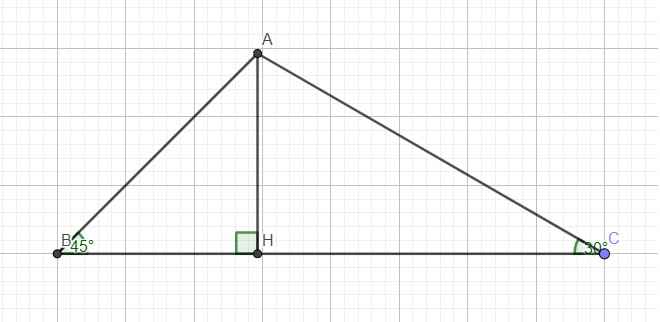
a.
Trong tam giác vuông ABH ta có:
\(cotB=\dfrac{BH}{AH}\Rightarrow BH=AH.cotB\)
Trong tam giác vuông ACH ta có:
\(cotC=\dfrac{CH}{AH}\Rightarrow CH=AH.cotC\)
\(\Rightarrow BH+CH=AH.cotB+AH.cotC\)
\(\Leftrightarrow BC=AH\left(cotB+cotC\right)\)
\(\Leftrightarrow AH=\dfrac{BC}{cotB+cotC}\) (đpcm)
b. Áp dụng công thức câu a:
\(AH=\dfrac{4}{cot45^0+cot30^0}=-2+2\sqrt{3}\) (cm)
\(S_{ABC}=\dfrac{1}{2}AH.BC=\dfrac{1}{2}.\left(-2+2\sqrt{3}\right).4=-4+4\sqrt{3}\approx2,93\left(cm^2\right)\)
AT
30 tháng 7 2021
\(\left(\sqrt{\dfrac{1+sin\alpha}{1-sin\alpha}}+\sqrt{\dfrac{1-sin\alpha}{1+sin\alpha}}\right).\dfrac{1}{\sqrt{1+tan^2\alpha}}\)
\(=\left(\sqrt{\dfrac{\left(1+sin\alpha\right)^2}{\left(1-sin\alpha\right)\left(1+sin\alpha\right)}}+\sqrt{\dfrac{\left(1-sin\alpha\right)^2}{\left(1+sin\alpha\right)\left(1-sin\alpha\right)}}\right).\dfrac{1}{\sqrt{1+\left(\dfrac{sin\alpha}{cos\alpha}\right)^2}}\)
\(=\left(\sqrt{\dfrac{\left(1+sin\alpha\right)^2}{1-sin^2\alpha}}+\sqrt{\dfrac{\left(1-sin\alpha\right)^2}{1-sin^2\alpha}}\right).\dfrac{1}{\sqrt{\dfrac{cos^2\alpha+sin^2\alpha}{cos^2\alpha}}}\)
\(=\left(\sqrt{\dfrac{\left(1+sin\alpha\right)^2}{cos^2\alpha}}+\sqrt{\dfrac{\left(1-sin\alpha\right)^2}{cos^2\alpha}}\right).\dfrac{1}{\sqrt{\dfrac{1}{cos^2\alpha}}}\)
\(=\left(\dfrac{1+sin\alpha}{cos\alpha}+\dfrac{1-sin\alpha}{cos\alpha}\right).\dfrac{1}{\dfrac{1}{cos\alpha}}=\dfrac{2}{cos\alpha}.cos\alpha=2\)