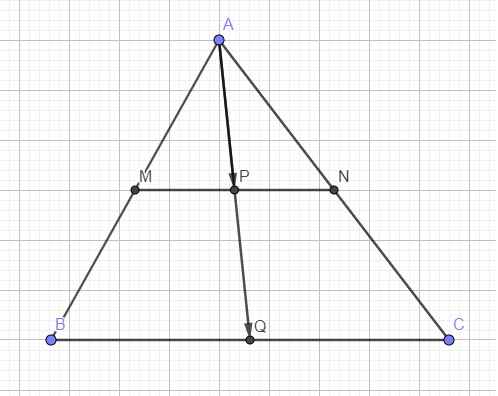
cho tam giác ABC.Gọi M,N lần lượt là trung điểm AB,AC.a)Gọi P,Q là trung điểm MN và BC .CMR a) A,P,Q thẳng hàng
b)Gọi E,F thỏa mãn \(\overrightarrow{ME}=\dfrac{1}{3}\overrightarrow{MN}\)
\(\overrightarrow{BF}=\dfrac{1}{3}\overrightarrow{BC}\)
cmr A,E,F thẳng hàng



minh dang nghi cau a con cau b minh ra r ban co can k
b)me=1/3mn bf=1/3bcmn//bc
=>me//bf
=>e la trung diem cua af
=> AEF thang hang
u a tuong tu