Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có \(\overrightarrow{AE}=\overrightarrow{AM}+\overrightarrow{ME}\)
\(=\frac{1}{2}\overrightarrow{AB}+\frac{1}{3}\overrightarrow{MN}\)
\(=\frac{1}{2}\overrightarrow{AB}+\frac{1}{6}\overrightarrow{BC}\)
\(=\frac{1}{2}\left(\overrightarrow{AB}+\frac{1}{3}\overrightarrow{BC}\right)\)
\(=\frac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{BF}\right)=\frac{1}{2}\overrightarrow{AF}\)
\(\Rightarrow A;E;F\) thẳng hàng

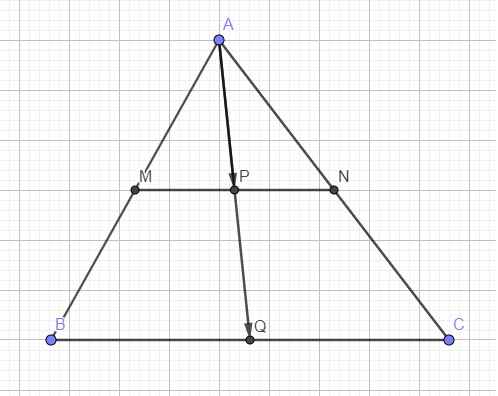
M là trung điểm AB \(\Rightarrow\overrightarrow{AM}=\dfrac{1}{2}\overrightarrow{AB}\)
N là trung điểm AC \(\Rightarrow\overrightarrow{AN}=\dfrac{1}{2}\overrightarrow{AC}\)
P là trung điểm MN \(\Rightarrow\overrightarrow{PM}+\overrightarrow{PN}=\overrightarrow{0}\) \(\Rightarrow\overrightarrow{PA}+\overrightarrow{AM}+\overrightarrow{PA}+\overrightarrow{AN}=\overrightarrow{0}\)
\(\Rightarrow\overrightarrow{AM}+\overrightarrow{AN}=-2\overrightarrow{PA}=2\overrightarrow{AP}\)
\(\Rightarrow\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}=2\overrightarrow{AP}\Rightarrow\overrightarrow{AP}=\dfrac{1}{4}\overrightarrow{AB}+\dfrac{1}{4}\overrightarrow{AC}\)
Q là trung điểm BC \(\Rightarrow\overrightarrow{QB}+\overrightarrow{QC}=\overrightarrow{0}\) \(\Rightarrow\overrightarrow{QA}+\overrightarrow{AB}+\overrightarrow{QA}+\overrightarrow{AC}=\overrightarrow{0}\)
\(\Rightarrow\overrightarrow{AB}+\overrightarrow{AC}=-2\overrightarrow{QA}=2\overrightarrow{AQ}\)
\(\Rightarrow\overrightarrow{AQ}=\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}=2\left(\dfrac{1}{4}\overrightarrow{AB}+\dfrac{1}{4}\overrightarrow{AC}\right)=2\overrightarrow{AP}\)
\(\Rightarrow A;P;Q\) thẳng hàng

Lời giải:
a) Vì $M$ là trung điểm của $EF$ nên \(\overrightarrow {ME}+\overrightarrow{MF}=0\), tương tự \(\overrightarrow{NB}+\overrightarrow{NC}=0\)
Từ đkđb ta cũng có \(AE=\frac{1}{3}AB;AF=\frac{3}{5}AC\)
Ý 1:
\(\left\{\begin{matrix} \overrightarrow{AM}=\overrightarrow{AE}+\overrightarrow{EM}\\ \overrightarrow{AM}=\overrightarrow{AF}+\overrightarrow{FM}\end{matrix}\right. \)
\(\Rightarrow 2\overrightarrow{AM}=\overrightarrow{AE}+\overrightarrow{AF}-(\overrightarrow{ME}+\overrightarrow{MF})=\overrightarrow{AE}+\overrightarrow{AF}\)
\(=\frac{1}{3}\overrightarrow{AB}+\frac{3}{5}\overrightarrow{AC}\)\(\Leftrightarrow \overrightarrow{AM}=\frac{1}{6}\overrightarrow{AB}+\frac{3}{10}\overrightarrow{AC}\)
Ý 2:
\(\left\{\begin{matrix} \overrightarrow{MN}=\overrightarrow{ME}+\overrightarrow{EB}+\overrightarrow{BN}\\ \overrightarrow{MN}=\overrightarrow{MF}+\overrightarrow{FC}+\overrightarrow{CN}\end{matrix}\right.\Rightarrow 2\overrightarrow{MN}=(\overrightarrow{ME}+\overrightarrow{MF})+\overrightarrow{EB}+\overrightarrow{FC}-(\overrightarrow{NB}+\overrightarrow{NC})\)
\(\Leftrightarrow 2\overrightarrow{MN}=\overrightarrow{EB}+\overrightarrow{FC}=\frac{2}{3}\overrightarrow{AB}+\frac{2}{5}\overrightarrow{AC}\)
\(\Leftrightarrow \overrightarrow{MN}=\frac{1}{3}\overrightarrow{AB}+\frac{1}{5}\overrightarrow{AC}\)
b)
Theo đkđb ta có: \(\overrightarrow{BG}=3\overrightarrow{CG}\)
\(\left\{\begin{matrix} \overrightarrow{AG}=\overrightarrow{AB}+\overrightarrow{BG}\\ \overrightarrow{AG}=\overrightarrow{AC}+\overrightarrow{CG}\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} \overrightarrow{AG}=\overrightarrow{AB}+\overrightarrow{BG}\\ 3\overrightarrow{AG}=3\overrightarrow{AC}+3\overrightarrow{CG}\end{matrix}\right.\)
\(\Rightarrow 2\overrightarrow{AG}=3\overrightarrow{AC}-\overrightarrow{AB}\Rightarrow \overrightarrow{AG}=\frac{3}{2}\overrightarrow{AC}-\frac{1}{2}\overrightarrow{AB}\)
Lại có:
\(\overrightarrow{EG}=\overrightarrow{EA}+\overrightarrow{AG}=\frac{-1}{3}\overrightarrow{AB}+\frac{3}{2}\overrightarrow{AC}-\frac{1}{2}\overrightarrow{AB}=\frac{3}{2}\overrightarrow{AC}-\frac{5}{6}\overrightarrow{AB}\)
\(\overrightarrow{FG}=\overrightarrow{FA}+\overrightarrow{AG}=\frac{-3}{5}\overrightarrow{AC}+\frac{3}{2}\overrightarrow{AC}-\frac{1}{2}\overrightarrow{AB}=\frac{9}{10}\overrightarrow{AC}-\frac{1}{2}\overrightarrow{AB}\)
c) Từ phần b ta thấy \(\frac{3}{5}\overrightarrow{EG}=\overrightarrow{FG}\Rightarrow E,G,F\) thẳng hàng.
minh dang nghi cau a con cau b minh ra r ban co can k
b)me=1/3mn bf=1/3bcmn//bc
=>me//bf
=>e la trung diem cua af
=> AEF thang hang
u a tuong tu