Chứng minh:
(x-y)3+z3 = (x+y+z)[(x+y)2-z(x+y)+z ]
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
9 tháng 7 2023
Bài 3:
a, (\(x\)+y+z)2
=((\(x\)+y) +z)2
= (\(x\) + y)2 + 2(\(x\) + y)z + z2
= \(x^2\) + 2\(xy\) + y2 + 2\(xz\) + 2yz + z2
=\(x^2\) + y2 + z2 + 2\(xy\) + 2\(xz\) + 2yz
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
9 tháng 7 2023
b, (\(x-y\))(\(x^2\) + y2 + z2 - \(xy\) - yz - \(xz\))
= \(x^3\) + \(xy^2\) + \(xz^2\) - \(x^2\)y - \(xyz\) - \(x^2\)z - y3
Đến dây ta thấy xuất hiện \(x^3\) - y3 khác với đề bài, em xem lại đề bài nhé
AH
Akai Haruma
Giáo viên
12 tháng 10 2021
Bài 1:
a. \(=[(3x+(4y-5z)][3x-(4y-5z)]=(3x)^2-(4y-5z)^2\)
\(=9x^2-(16y^2-40yz+25z^2)=9x^2-16y^2+40yz-25z^2\)
b.
\(=(3a-1)^2+2(3a-1)(3a+1)+(3a+1)^2=[(3a-1)+(3a+1)]^2=(6a)^2=36a^2\)
AH
Akai Haruma
Giáo viên
12 tháng 10 2021
Bài 2:
\((x+y+z)^3=[(x+y)+z]^3=(x+y)^3+3(x+y)^2z+3(x+y)z^2+z^3\)
\(=[x^3+y^3+3xy(x+y)]+3(x+y)z(x+y+z)+z^3\)
\(=x^3+y^3+z^3+3xy(x+y)+3(x+y)z(x+y+z)\)
\(=x^3+y^3+z^3+3(x+y)(xy+zx+zy+z^2)\)
\(=x^3+y^3+z^3+3(x+y)(z+x)(z+y)\) (đpcm)
4 tháng 9 2021
a: Ta có: \(\left(x+y\right)^2\)
\(=x^2+2xy+y^2\)
\(\Leftrightarrow x^2+y^2=\dfrac{\left(x+y\right)^2}{2xy}\ge\dfrac{\left(x+y\right)^2}{2}\forall x,y>0\)
CM
12 tháng 10 2017
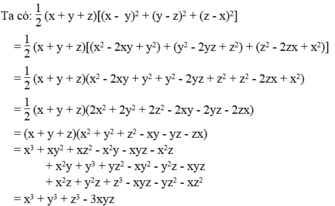
Vế trái bằng vế phải nên đẳng thức được chứng minh.
Nếu x ≥ 0, y ≥ 0, z ≥ 0 thì:
x + y + z ≥ 0
x - y 2 + y - z 2 + z - x 2 ≥ 0
Suy ra:
x 3 + y 3 + z 3 - 3 x y z ≥ 0 ⇔ x 3 + y 3 + z 3 ≥ 3 x y z
Hay: x 3 + y 3 + z 3 3 ≥ x y z
TX
0
DD
0
BZ
0
NN
3
21 tháng 9 2016
x^3+y^3+z^3-3xyz=1/2(x+y+z)[(x-y)^2+(y-z)^2+(z-x)^2]
2 cái bằng nhau