Cho hình thang ABCD biết A=B=90o;AB=BC\(=\dfrac{1}{2}AD\)
Tính các góc trong hình thang ?
Cm:\(AC\perp CD\)
MIK ĐAG CẦN GẤP GIÚP VỚI !!! 
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
24 tháng 7 2021
Kẻ đường cao BE ứng với CD \(\Rightarrow BE=4\left(cm\right)\)
Trong tam giác vuông BCE ta có:
\(\widehat{EBC}=90^0-\widehat{C}=90^0-45^0=45^0\)
\(\Rightarrow\widehat{EBC}=\widehat{C}\Rightarrow\Delta BCE\) vuông cân tại E
\(\Rightarrow EC=BE=4\left(cm\right)\)
Tứ giác ABED là hình chữ nhật (tứ giác có 3 góc vuông)
\(\Rightarrow AB=DE\)
Ta có:
\(AB+CD=10\left(cm\right)\)
\(\Leftrightarrow AB+DE+EC=10\)
\(\Leftrightarrow2AB+4=10\)
\(\Rightarrow AB=3\left(cm\right)\)
\(\Rightarrow DE=AB=3cm\Rightarrow CD=DE+EC=7\left(cm\right)\)
CM
3 tháng 1 2020
Chọn đáp án A.
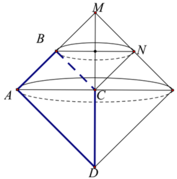
Gọi M là giao điểm của AB và CD. Từ B kẻ đường thẳng song song với AC, cắt CM tại N.
Khi quay ABCD quanh trục CD ta được hai phần:
+ Tam giác ACD sinh ra khối nón với bán kính đáy
AT
12 tháng 6 2021
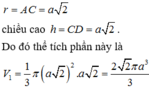
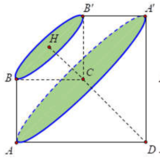
Ta có: \(AH^2=HD.HB=18.8=144\Rightarrow AH=12\) (cm)
\(\Rightarrow AD=\sqrt{AH^2+HD^2}=\sqrt{12^2+18^2}=6\sqrt{13}\)
\(AB=\sqrt{12^2+8^2}=4\sqrt{13}\)
Ta có: \(DH^2=HA.HC\Rightarrow CH=\dfrac{DH^2}{HA}=\dfrac{18^2}{12}=27\)
\(\Rightarrow CD=\sqrt{CH^2+HD^2}=\sqrt{27^2+18^2}=9\sqrt{13}\)
\(\Rightarrow S_{ABCD}=\dfrac{1}{2}\left(AB+CD\right).AD=\dfrac{1}{2}\left(4\sqrt{13}+9\sqrt{13}\right).6\sqrt{13}\)
\(=507\left(cm^2\right)\)
AH
Akai Haruma
Giáo viên
15 tháng 9 2021
Lời giải:
a. $BD\perp BC, BD=BC$ nên tam giác $BDC$ vuông cân tại $B$
$\Rightarrow \widehat{C}=45^0$
$\widehat{ABC}=180^0-\widehat{C}=180^0-45^0=135^0$
b.
Ta có: $\widehat{ABD}=\widehat{ABC}-\widehat{DBC}=135^0-90^0=45^0$ nên tam giác $ABD$ vuông cân tại $A$
$\Rightarrow AD=AB=3$
Áp dụng định lý Pitago:
$BD=\sqrt{AB^2+AD^2}=\sqr{3^2+3^2}=3\sqrt{2}$ (cm)
$BC=BD=3\sqrt{2}$ (cm)
Tam giác $BDC$ vuông cân tại $B$ nên áp dụng định lý Pitago:
$DC=\sqrt{BC^2+BD^2}=\sqrt{(3\sqrt{2})^2+(3\sqrt{2})^2}=6$ (cm)
HN
0
9 tháng 1 2023
Gọi K là trung điểm của HD
Xet ΔHDC có HK/HD=HM/HC
nên KM//DC
=>KM vuông góc với AD
Xét ΔADM có
MK,DH là các đường cao
MK cắt DH tại K
Do đó: K làtrực tâm
=>AK vuông góc với DM
Xét tứ giác ABMK có
AB//MK
AB=MK
Do đó; ABMK là hình bình hành
=>AK//BM
=>BM vuông góc với DM
15 tháng 1 2023
Gọi K là trung điểm của HD
Xet ΔHDC có HK/HD=HM/HC
nên KM//DC
=>KM vuông góc với AD
Xét ΔADM có
MK,DH là các đường cao
MK cắt DH tại K
Do đó: K làtrực tâm
=>AK vuông góc với DM
Xét tứ giác ABMK có
AB//MK
AB=MK
Do đó; ABMK là hình bình hành
=>AK//BM
=>BM vuông góc với DM
Gọi E là trung điểm của AD
=>AE//BC và AE=BC
Xét tứ giác ABCE có
BC//AE
BC=AE
Do đó: ABCE là hình bình hành
mà BC=AB
nên ABCE là hình thoi
mà \(\widehat{CBA}=90^0\)
nên ABCE là hình vuông
=>\(\widehat{BCE}=\widehat{CEA}=90^0\) và CE=AE=ED
Xét ΔCED vuông tại E có EC=ED
nên ΔCED vuông cân tại E
=>\(\widehat{D}=45^0\)
=>\(\widehat{C}=135^0\)
b: Xét ΔACD có
CE là đường trung tuyến
CE=AD/2
Do đó:ΔACD vuông tại C