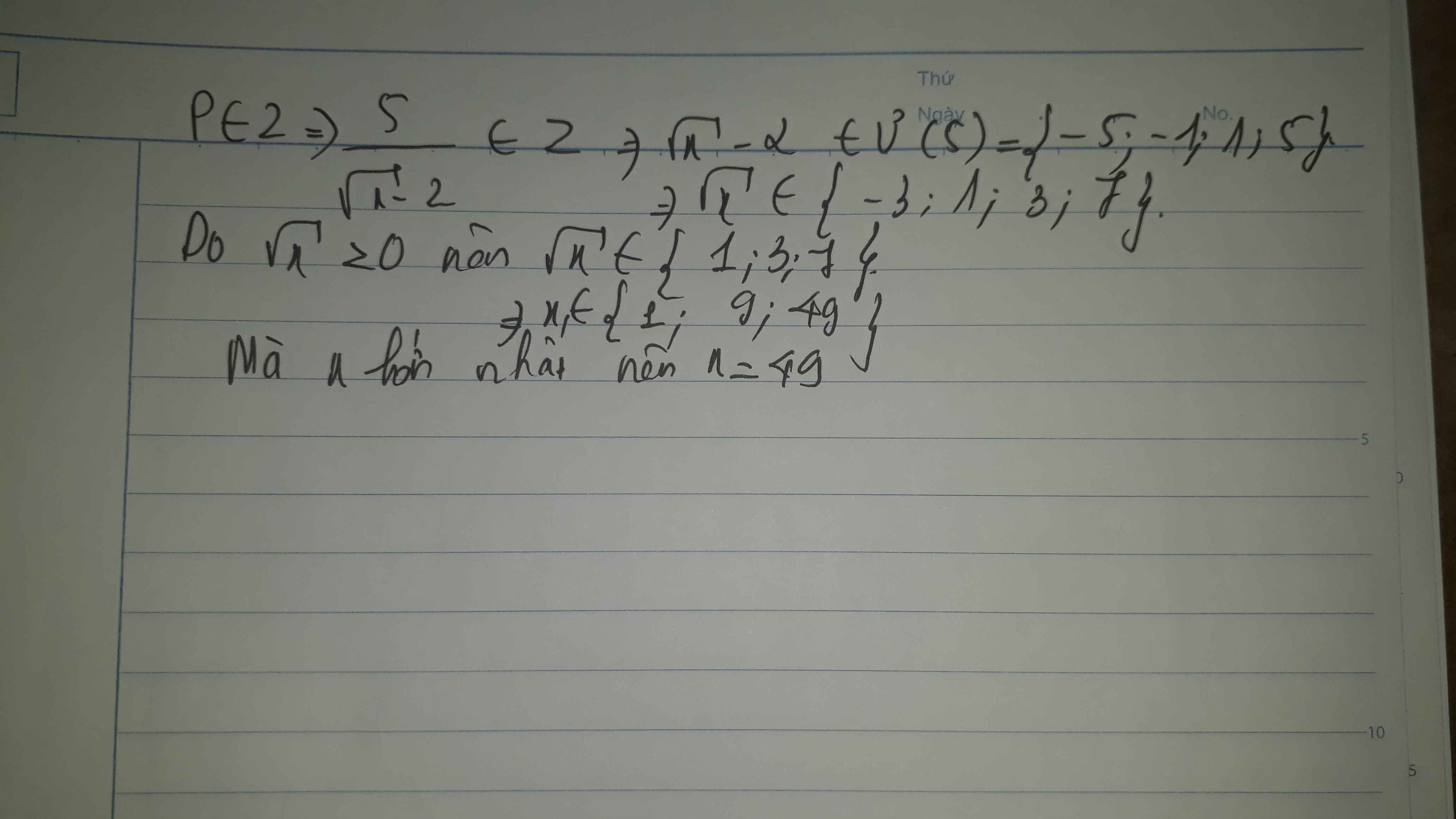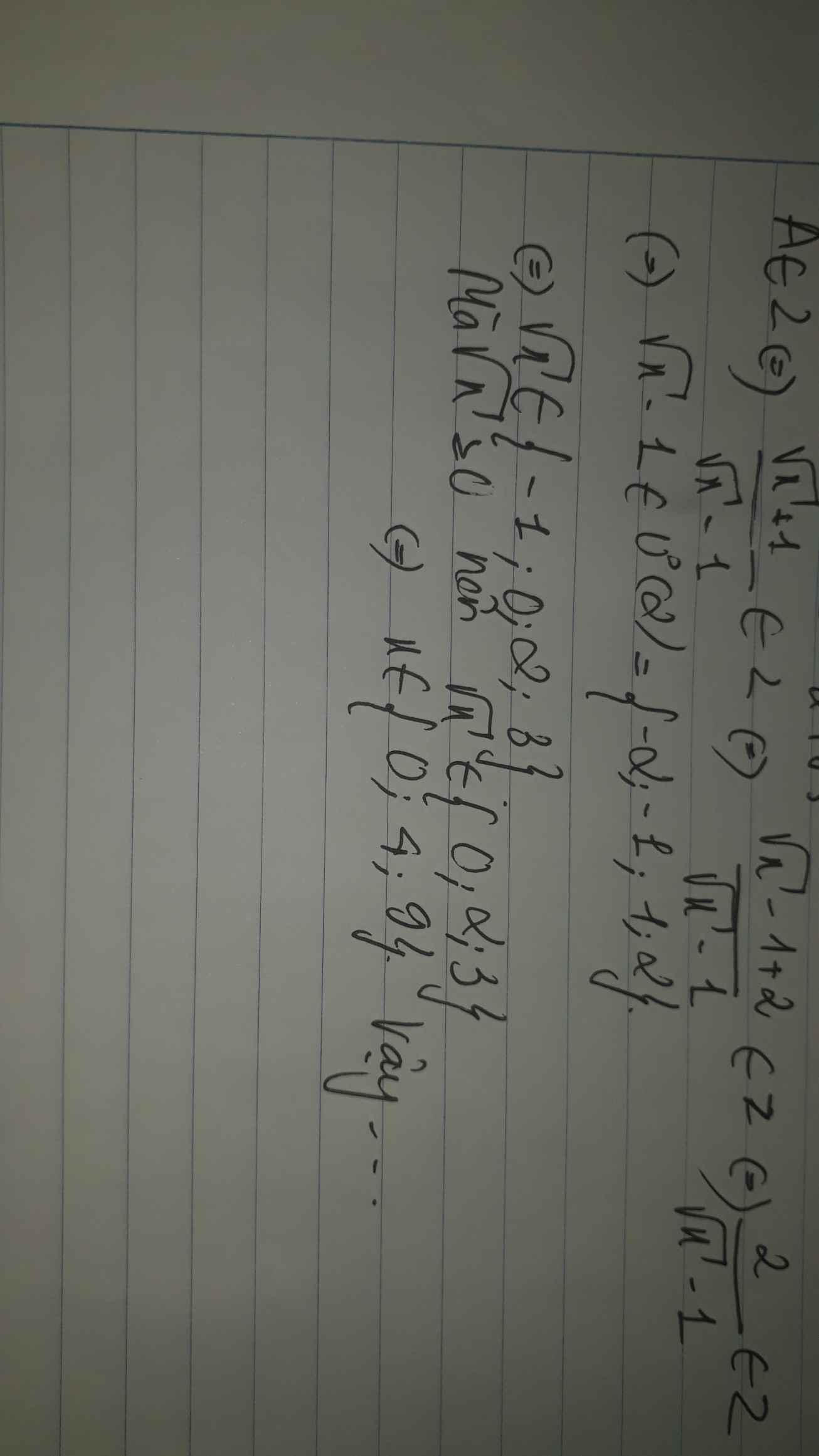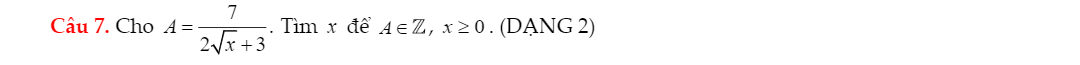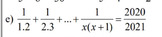Gíup em chi tiết vs
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
26 tháng 8 2021
Để \(P\in Z\) thì
\(\sqrt{x}-2\inƯ\left(5\right)=\left\{1;-1;5;-5\right\}\)
Mà \(x\in N,x\ne4\)
\(\Rightarrow x\in\left\{9;1;49\right\}\)
Vậy giá trị x lớn nhất cần tìm là: x=49
26 tháng 8 2021
\(A=\dfrac{\sqrt{x}+1}{\sqrt{x}-1}=\dfrac{\sqrt{x}-1}{\sqrt{x}-1}+\dfrac{2}{\sqrt{x}-1}=1+\dfrac{2}{\sqrt{x}-1}\)
Để \(A\in Z\) thì \(\sqrt{x}-1\inƯ\left(2\right)=\left\{1;-1;2;-2\right\}\)
Mà \(x\in Z,x\ge0,x\ne1\)
\(\Rightarrow x\in\left\{4;0;9\right\}\)
AH
Akai Haruma
Giáo viên
26 tháng 8 2021
Lời giải:
Dễ thấy $2\sqrt{x}+3>0; 7>0$ nên $A>0$
Mặt khác:
$2\sqrt{x}\geq 0\Rightarrow 2\sqrt{x}+3\geq 3$
$\Rightarrow A=\frac{7}{2\sqrt{x}+3}\leq \frac{7}{3}$
Vậy $0< A< \frac{7}{3}$
$A\in\mathbb{Z}\Leftrightarrow A\in\left\{1;2\right\}$
$\Leftrightarrow \frac{7}{2\sqrt{x}+3}\in \left\{1;2\right\}$
$\Leftrightarrow x\in\left\{4; \frac{1}{16}\right\}$
26 tháng 8 2021
Để A là số nguyên thì \(7⋮2\sqrt{x}+3\)
\(\Leftrightarrow2\sqrt{x}+3=7\)
\(\Leftrightarrow2\sqrt{x}=4\)
hay x=4
5 tháng 3 2022
\(\Leftrightarrow1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{x}-\dfrac{1}{x+1}=\dfrac{2020}{2021}\)
\(\Leftrightarrow1-\dfrac{1}{x+1}=\dfrac{2020}{2021}\Leftrightarrow\dfrac{x}{x+1}=\dfrac{2020}{2021}\Rightarrow2021x=2020x+2020\Leftrightarrow x=2020\)
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 4 2021
29
Phương trình tương đương:
\(\left(2y+1\right)\left(4y-3\right)=x^2\left(2-x\right)\) (1)
Do y nguyên dương \(\Rightarrow4y-3>0\Rightarrow\left(2y+1\right)\left(4y-3\right)>0\)
Đồng thời \(x^2>0\) với mọi x nguyên dương
Nếu \(x\ge2\Rightarrow2-x\le0\Rightarrow\left\{{}\begin{matrix}VT>0\\VP\le0\end{matrix}\right.\) không tồn tại x; y nguyên dương thỏa mãn (loại)
\(\Rightarrow x< 2\) , mà \(x\) nguyên dương \(\Rightarrow x=1\)
Thế vào (1):
\(\Leftrightarrow\left(2y+1\right)\left(4y-3\right)=1\)
\(\Rightarrow\left\{{}\begin{matrix}2y+1=1\\4y-3=1\end{matrix}\right.\) không tồn tại y nguyên dương thỏa mãn
Vậy pt đã cho không có nghiệm nguyên dương
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 4 2021
30.
\(\Leftrightarrow y\left(2x^2+1\right)=4x^2+5\)
\(\Leftrightarrow y=\dfrac{4x^2+5}{2x^2+1}=2+\dfrac{3}{2x^2+1}\)
Do y nguyên \(\Rightarrow\dfrac{3}{2x^2+1}\) nguyên
\(\Rightarrow2x^2+1=Ư\left(3\right)\)
Mà \(2x^2+1\ge1\Rightarrow\left[{}\begin{matrix}2x^2+1=1\\2x^2+1=3\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=0\left(loại\right)\\x=-1\left(loại\right)\\x=1\Rightarrow y=3\end{matrix}\right.\)
\(\Rightarrow x+y=1+3=\)
12 tháng 8 2021
Câu 3:
a) Lưu huỳnh (S) có hóa trị II. Hidro (H) có hóa trị I.
-> Ta sẽ có hợp chất: \(H^I_aS^{II}_b\) (a,b: nguyên, dương)
Theo quy tắc hóa trị ta có:
I.a=II.b
=>a/b=II/I=2/1
=>a=2; b=1
=> CTHH là H2S
13 tháng 8 2021
Câu 3b)
- Na có hóa trị (I) và CO3 có hóa trị (II).
- Ta đặt: \(Na^I_x\left(CO_3\right)^{II}_y\) (x,y: nguyên, dương)
Theo QT hóa trị ta sẽ có được:
x.I=II.y
<=>x/y=II/I=2/1
=>x=2; y=1
=> CTHH sẽ là Na2CO3