Giải gấp giúp e với ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LT
0
19 tháng 12 2023
a: \(VP=a^3+b^3+c^3-3bac\)
\(=\left(a+b\right)^3+c^3-3ab\left(a+b\right)-3abc\)
\(=\left(a+b+c\right)\left[\left(a+b\right)^2-c\left(a+b\right)+c^2\right]-3ab\left(a+b+c\right)\)
\(=\left(a+b+c\right)\left(a^2+2ab+b^2-ac-bc+c^2-3ab\right)\)
\(=\left(a+b+c\right)\left(a^2+b^2+c^2-ab-bc-ac\right)=VT\)
b: \(VT=\left(3a+2b-1\right)\left(a+5\right)-2b\left(a-2\right)\)
\(=3a^2+15a+2ab+10b-a-5-2ab+4b\)
\(=3a^2+14a+14b-5\)
\(VP=\left(3a+5\right)\left(a+3\right)+2\left(7b-10\right)\)
\(=3a^2+9a+5a+15+14b-20\)
\(=3a^2+14a+14b-5\)
=>VT=VP
c: \(VT=a\left(b-x\right)+x\left(a+b\right)\)
\(=ab-ax+ax+bx\)
\(=ab+bx=b\left(a+x\right)=VP\)
d: \(VT=a\left(b-c\right)-b\left(a+c\right)+c\left(a-b\right)\)
\(=ab-ac-ab-bc+ca-cb\)
\(=-2bc\)
=VP
AH
Akai Haruma
Giáo viên
2 tháng 1
Lời giải:
a. Xét tứ giác $ADHE$ có 3 góc vuông $\widehat{A}=\widehat{D}=\widehat{E}=90^0$ nên tứ giác $ADHE$ là hình chữ nhật.
b.
Xét tam giác vuông $BDH$ vuông tại $D$ có $DI$ là đường trung tuyến ứng với cạnh huyền $BH$ nên $DI=\frac{BH}{2}=IH$
$\Rightarrow DIH$ là tam giác vuông tại $I$
$\Rightarrow \widehat{IDH}=\widehat{IHD}$ (1)
$ADHE$ là hình chữ nhật nên $\widehat{HDE}=\widehat{HAE}=\widehat{HAC}$ (2)
Từ $(1); (2)\Rightarrow \widehat{IDH}+\widehat{HDE}=\widehat{IHD}+\widehat{HAC}$
$\Rightarrow \widehat{IDE}=\widehat{IHD}+\widehat{HAC}$.
Mà $\widehat{IHD}=\widehat{HCA}$ (2 góc đồng vị)
$\Rightarrow \widehat{IDE}=\widehat{HCA}+\widehat{HAC}=180^0-\widehat{AHC}=180^0-90^0=90^0$
$\Rightarrow DI\perp DE$
c. Tương tự phần a ta suy ra $DE\perp EK$
Vậy $DI\perp DE, EK\perp DE$
$\Rightarrow DI\parallel EK$ và $DI, EK$ cùng vuông góc với $DE$
$\Rightarrow DIKE$ là hình thang vuông.
d.
Có: $DI=\frac{BH}{2}\Rightarrow BH=2DI=2.1=2$ (cm)
$EK=\frac{CH}{2}\Rightarrow CH=2EK=8$ (cm)
$\Rightarrow BC=BH+CH=2+8=10$ (cm)
$S_{ABC}=AH.BC:2=6.10:2=30$ (cm2)
LC
1
21 tháng 11 2023
a: Xét ΔHAC vuông tại H và ΔABC vuông tại A có
\(\widehat{C}\) chung
Do đó: ΔHAC~ΔABC
b: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=15^2+20^2=625\)
=>BC=25
Xét ΔABC vuông tại A có AH là đường cao
nên \(\left\{{}\begin{matrix}BH\cdot BC=BA^2\\AH\cdot BC=AB\cdot AC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH\cdot25=15^2=225\\AH\cdot25=15\cdot20=300\end{matrix}\right.\)
=>BH=9; AH=12
LT
1
1 tháng 7 2023
a: góc AEH=góc ADH=góc DAE=90 độ
=>AEHD là hcn
b: XétΔAEH vuông tại E và ΔAHC vuông tại H có
góc EAH chung
=>ΔAEH đồng dạng với ΔAHC
c: ΔAHC vuông tại H có HE là đường cao
nên HE^2=AE*EC
NT
1
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 9 2021
1.
\(D=R\backslash\left\{\dfrac{\pi}{6}+\dfrac{k\pi}{3}\right\}\) là miền đối xứng
\(f\left(-x\right)=\left(-x^3-x\right)tan\left(-3x\right)=\left(x^3+x\right)tan3x=f\left(x\right)\)
Hàm chẵn
2.
\(D=R\)
\(f\left(-x\right)=\left(-2x+1\right)sin\left(-5x\right)=\left(2x-1\right)sin5x\ne\pm f\left(x\right)\)
Hàm không chẵn không lẻ
3.
\(D=R\backslash\left\{\dfrac{\pi}{6}+\dfrac{k\pi}{3}\right\}\) là miền đối xứng
\(f\left(-x\right)=tan\left(-3x\right).sin\left(-5x\right)=-tan3x.\left(-sin5x\right)=tan3x.sin5x=f\left(x\right)\)
Hàm chẵn
4.
\(D=R\)
\(f\left(-x\right)=sin^2\left(-2x\right)+cos\left(-10x\right)=sin^22x+cos10x=f\left(x\right)\)
Hàm chẵn
5.
\(D=R\backslash\left\{k\pi\right\}\) là miền đối xứng
\(f\left(-x\right)=\dfrac{-x}{sin\left(-x\right)}=\dfrac{-x}{-sinx}=\dfrac{x}{sinx}=f\left(x\right)\)
Hàm chẵn
ND
2
14 tháng 9 2021
12 : {390 : [500 - (125 + 35 . 7)]}
= 12 : {390 : [500 - (125 + 245)]}
= 12 : [390 : (500 - 370)]
= 12 : (390 : 130)
= 12 : 3
= 4
14 tháng 9 2021
12 : { 390 : [ 500 - ( 125 + 35. 7 ) ] }
= 12 : { 390 : [ 500 - ( 125 + 245 ) ] }
= 12 : { 390 : [ 500 - 370 ] }
= 12 : { 390 : 130 }
= 12 : 3
= 4
LT
0
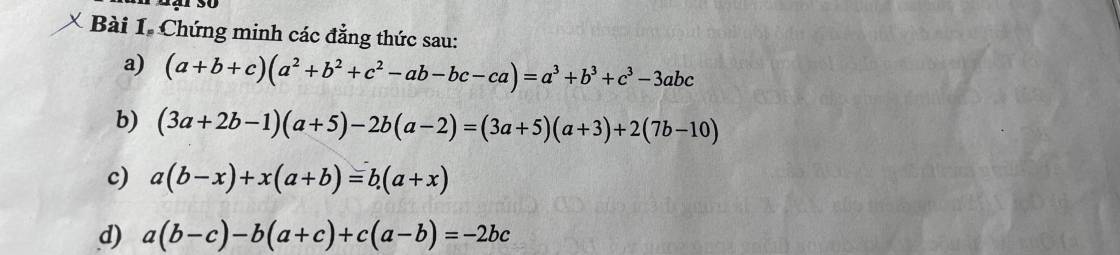
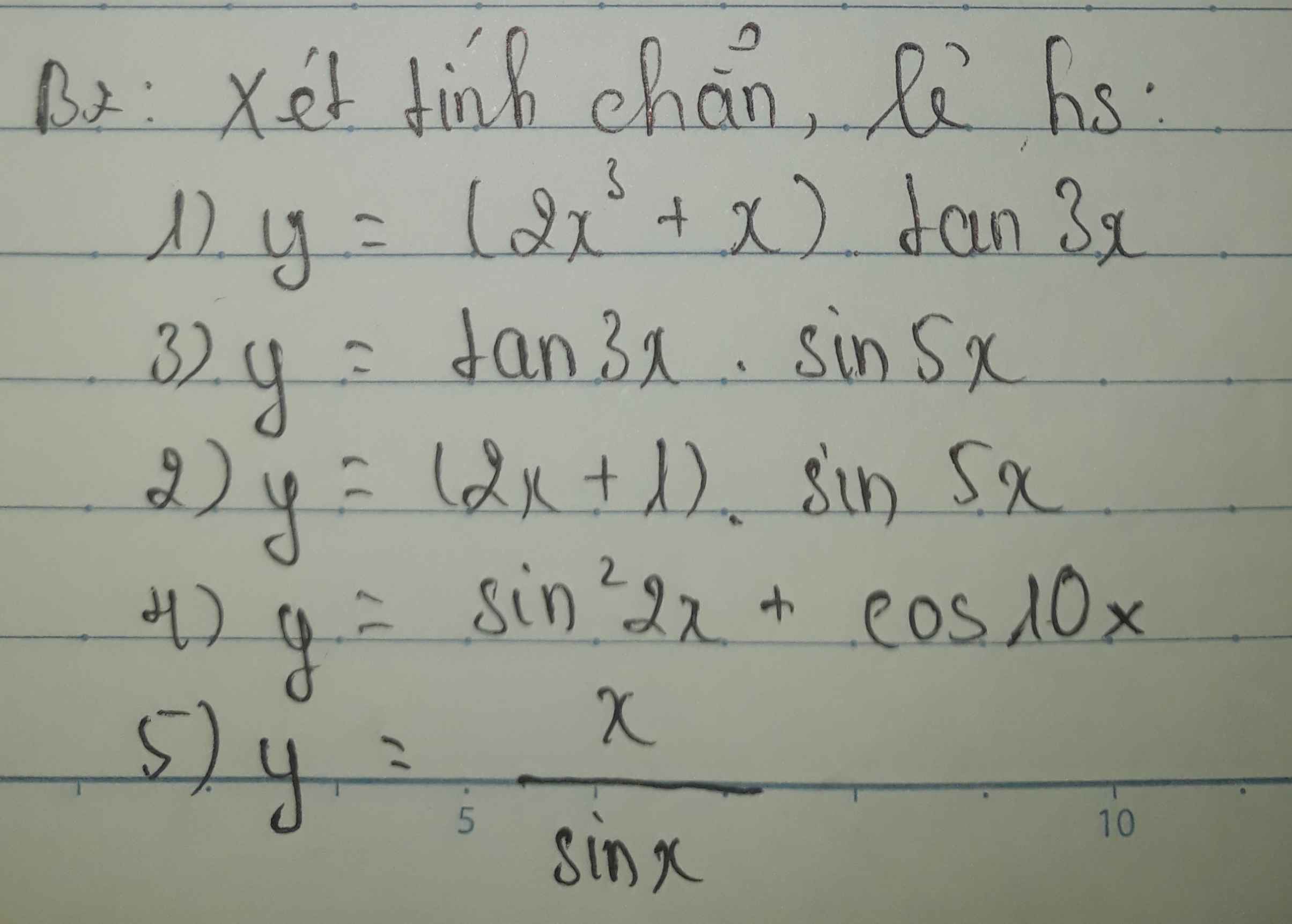
nAl = 0,8 (mol); nFe3O4 = 0,5 (mol)
PTHH :8Al + 3Fe3O4 --to--> 4Al2O3 + 9Fe
Nhận thấy : \(\dfrac{n_{Al}}{8}< \dfrac{nFe_3O_4}{3}\left(0,1< 0,16\right)\)
=> Al hết; fe3o4 dư
BT Oxi : nAl2o3 = 1/2 nAl = 0,4 (mol) => nFe3O4 pứ = 3/4 nAl2o3 = 0,3 (mol)
=> nFe3o4 dư = 0,5 - 0,3 = 0,2 (mol)
BT Fe : nFe = 3nFe3o4 pứ = 0,9 (mol)
Hồn hợp spu gồm : 0,4 mol Al2O3; 0,9 mol Fe và 0,2 mol Fe3O4 dư
Khi chia hỗn hợp ra làm 4 phần, mỗi phần sẽ gồm: 0,1 mol Al2O3; 0,225 mol Fe và 0,05 mol Fe3O4 dư
1. PTHH : \(Al_2O_3+6HCl-->2AlCl_3+3H_2O\)
\(Fe_3O_4+8HCl-->FeCl_2+2FeCl_3+4H_2O\)
\(Fe+2HCl-->FeCl_2+H_2\)
nH2 = nFe = 0,225 (mol)
=> VH2 = 0,225.22,4 = 5,04 (l)
2. \(Al_2O_3+3H_2SO_4-->Al_2\left(SO_4\right)_3+3H_2O\) (1)
\(Fe_3O_4+4H_2SO_4-->FeSO_4+Fe_2\left(SO_4\right)_3+4H_2O\) (2)
\(Fe+H_2SO_4-->FeSO_4+H_2\) (3)
\(Fe+Fe_2\left(SO_4\right)_3-->3FeSO_4\) (4)
nH2SO4 (1;2) = 3nAl2O3 + 4nFe3O4 = 3.0,1 + 4.0,05 = 0,5 (mol)
Theo pthh (2) : nFe2(SO4)3 = nFe3O4 = 0,05 (mol)
Theo pthh (4) : nFe(4) = nFe2(SO4)3 = 0,05 (mol)
=> nFe(3) = tổng nFe - nFe(4) = 0,225 - 0,05 = 0,175 (mol)
=> nH2SO4(3) = nFe(3) = 0,175 (mol)
=> tổng nH2SO4 = nH2SO4 (1;2) + nH2SO4(3) = 0,5 + 0,175 = 0,675 (mol)
V(H2SO4) = 0,675/2 = 0,3375 (l) = 337,5 (ml)
của mik giải theo đề cần dùng tối thiểu bao nhiêu ml dung dịch h2so4 nha
3. PTHH : \(Al_2O_3+2NaOH-->2NaAlO_2+H_2O\)
mCR còn lại = mFe + mFe3O4 = 0,225.56 + 0,05.232 = 24,2 (g)
4. PTHH : \(Al_2O_3+6HNO_3-->2Al\left(NO_3\right)_3+3H_2O\)
\(Fe_3O_4+10HNO_3-->3Fe\left(NO_3\right)_3+NO_2+5H_2O\)
\(Fe+6HNO_3-->Fe\left(NO_3\right)_3+3NO_2+3H_2O\)
nNO2 = nFe3O4 + 3nFe = 0,05 + 3.0,225 = 0,725 (mol)
=> V(NO2) = 0,725.22,4 = 16,24 (l)
bài dài quá check lại giùm mik nha