một vật dao động điều hòa với chu kì T= 3,14s. xác định pha dao động của vật khi nó qua vị trí x=2 cm với vận tốc v=0,04 m/s
A\(\dfrac{\pi}{3}\) rad
B \(\dfrac{\pi}{4}\)rad
C \(\dfrac{\pi}{6}\)rad
D\(\dfrac{-\pi}{4}\) rad
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
7 tháng 11 2023
\(a=-8m/s^2\) và pha dao động \(\varphi=\dfrac{\pi}{4}\)
\(\omega=2\pi f=2\pi\cdot2=4\pi\)
Mà \(a=-\omega^2Acos\varphi\) nên \(-8=-\left(4\pi\right)^2\cdot Acos\dfrac{\pi}{4}\)
\(\Rightarrow A=\dfrac{-8}{-4^2\cdot10\cdot\dfrac{\sqrt{2}}{2}}=\dfrac{\sqrt{2}}{20}\left(m\right)\approx7,1cm\)
HT
30 tháng 1 2021
\(\omega=\dfrac{2\pi}{T}=\dfrac{2\pi}{3,14}=...\left(rad/s\right)\)
\(A^2=x^2+\dfrac{v^2}{\omega^2}\Rightarrow A=...\left(cm\right)\)
\(\Rightarrow\dfrac{x}{A}=\dfrac{2}{A}\Rightarrow x=...A\)
\(\Rightarrow\cos\varphi=\dfrac{x}{A}\Rightarrow\varphi=...\left(rad\right)\)
thông cảm máy tính ko có ở đây nên bạn tự tính nhé, có gì ko hiểu hỏi tui
HQ
Hà Quang Minh
Giáo viên
27 tháng 8 2023
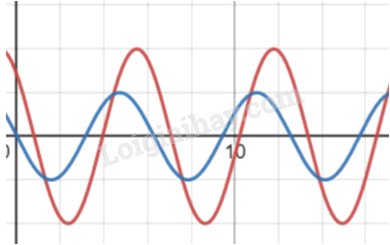
Dao động 1 vẽ với biên độ A và chu kì T
Dao động 2 có cùng chu kì với dao động 1 và biên độ \(A_2=2A\) vị trí đầu tiên của dao động thứ hai bằng \(\dfrac{\sqrt{2}}{2}A_2\) và ở thời điểm \(\dfrac{T}{8}\) thì dao động 2 sẽ đi qua vị trí cân bằng.
Cứ thế tiếp tục vẽ 2 chu kì dao động của hai dao động
Đường màu xanh là dao động thứ nhất, đường màu đỏ là dao động thứ 2
29 tháng 8 2023
Pha ban đầu là \(4pi\cdot t-\dfrac{pi}{2}\)
Tần số là \(f=\dfrac{4pi}{2pi}=2\)
Chu kì là \(T=\dfrac{1}{f}=\dfrac{1}{2}\)
Tần số góc là \(w=2pi:\dfrac{1}{2}=4pi\)
M
1 tháng 9 2023
Để tính giá trị của t, ta sử dụng công thức:
t = φ / ω
Trong đó:
t là thời gian tính từ lúc con lắc bắt đầu dao động.φ là pha ban đầu của dao động.ω là tần số góc của dao động.Theo đề bài, tần số góc ω = 5π rad/s và pha ban đầu φ = -π/3 rad. Thay vào công thức trên, ta có:
t = (-π/3) / (5π) = -1/15 s
Tuy nhiên, thời gian không thể có giá trị âm, vì vậy giá trị của t là 1/15 s.
H9
HT.Phong (9A5)
CTVHS
5 tháng 8 2023
Tham khảo:
\(v=-\omega Acos\left(\omega t+\varphi\right)\)
\(\Rightarrow-60=-\omega\cdot6\cdot cos\left(\omega t+\dfrac{\pi}{6}\right)\)
\(\Leftrightarrow-60=-\dfrac{\varphi}{t}\cdot6\cdot cos\left(\dfrac{\varphi}{t}\cdot t+\dfrac{\pi}{6}\right)\)
\(\Leftrightarrow-60=-\dfrac{\pi}{6}\cdot\dfrac{1}{t}\cdot6\cdot cos\left(\dfrac{\pi}{6}\cdot\dfrac{1}{t}\cdot t+\dfrac{\pi}{6}\right)\)
\(\Leftrightarrow-60=-\dfrac{\pi}{6}\cdot\dfrac{1}{t}\cdot6\cdot cos\left(\dfrac{\pi}{6}+\dfrac{\pi}{6}\right)\)
\(\Leftrightarrow\dfrac{1}{t}=\dfrac{120}{\pi}\Leftrightarrow t=\dfrac{\pi}{120}\left(s\right)\)
Mà: \(\omega=\dfrac{\varphi}{t}=\dfrac{\dfrac{\pi}{6}}{\dfrac{\pi}{120}}=\dfrac{120}{6}=20\left(rad/s\right)\)
Chu kì của dao động là:
\(T=\dfrac{2\pi}{\omega}=\dfrac{2\pi}{20}=\dfrac{\pi}{10}\left(s\right)\)
23 tháng 10 2023
a)\(v_{max}=\omega A=5\pi^2\approx50\left(cm/s\right)\)
Tần số góc: \(\omega=\pi\left(rad\right)\)
Chu kì: \(T=\dfrac{2\pi}{\omega}=\dfrac{2\pi}{\pi}=2s\)
Pha ban đầu của vận tốc: \(\varphi=\dfrac{\pi}{3}\)
b)Tại thời điểm \(t=0,25s\):
\(\Rightarrow v=5\pi cos\left(\pi\cdot0,25+\dfrac{\pi}{3}\right)\approx-4,065m/s\)
\(A^2=x^2+\dfrac{v^2}{\left(\omega^2\right)}=8\Rightarrow A=2\sqrt{2}\Rightarrow x=Acos\left(\varphi t\right)\Rightarrow cos\left(\varphi t\right)=\dfrac{x}{A}=\dfrac{\sqrt{2}}{2}\Rightarrow\varphi t=\dfrac{-\pi}{4}\)