Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(a=-8m/s^2\) và pha dao động \(\varphi=\dfrac{\pi}{4}\)
\(\omega=2\pi f=2\pi\cdot2=4\pi\)
Mà \(a=-\omega^2Acos\varphi\) nên \(-8=-\left(4\pi\right)^2\cdot Acos\dfrac{\pi}{4}\)
\(\Rightarrow A=\dfrac{-8}{-4^2\cdot10\cdot\dfrac{\sqrt{2}}{2}}=\dfrac{\sqrt{2}}{20}\left(m\right)\approx7,1cm\)

Chu kì dao động của vật chỉ phụ thuộc vào đặc tính của hệ nên luôn là 0,3 s.
Đáp án A

Đáp án A
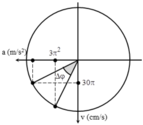
+ Biểu diễn các vị trí tương ứng trên đường tròn. Để thõa mãn điều kiện bài toán thì khoảng thời 1 60 s gian tương ứng với góc quét Δφ
→ Từ hình vẽ, ta có:
arcos 30 π ωA − arsin 300 π 2 ω 2 A 360 0 T = arcos 30 π 6 ω − arsin 300 π 2 6 ω 2 ω = 1 60
→ Phương trình trên cho ta nghiệm ω = 31,6 rad/s → T = 0,2 s
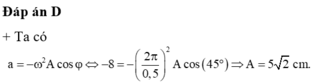
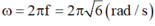
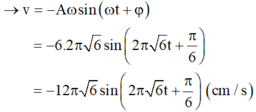
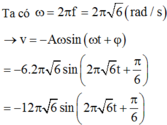

Tham khảo:
\(v=-\omega Acos\left(\omega t+\varphi\right)\)
\(\Rightarrow-60=-\omega\cdot6\cdot cos\left(\omega t+\dfrac{\pi}{6}\right)\)
\(\Leftrightarrow-60=-\dfrac{\varphi}{t}\cdot6\cdot cos\left(\dfrac{\varphi}{t}\cdot t+\dfrac{\pi}{6}\right)\)
\(\Leftrightarrow-60=-\dfrac{\pi}{6}\cdot\dfrac{1}{t}\cdot6\cdot cos\left(\dfrac{\pi}{6}\cdot\dfrac{1}{t}\cdot t+\dfrac{\pi}{6}\right)\)
\(\Leftrightarrow-60=-\dfrac{\pi}{6}\cdot\dfrac{1}{t}\cdot6\cdot cos\left(\dfrac{\pi}{6}+\dfrac{\pi}{6}\right)\)
\(\Leftrightarrow\dfrac{1}{t}=\dfrac{120}{\pi}\Leftrightarrow t=\dfrac{\pi}{120}\left(s\right)\)
Mà: \(\omega=\dfrac{\varphi}{t}=\dfrac{\dfrac{\pi}{6}}{\dfrac{\pi}{120}}=\dfrac{120}{6}=20\left(rad/s\right)\)
Chu kì của dao động là:
\(T=\dfrac{2\pi}{\omega}=\dfrac{2\pi}{20}=\dfrac{\pi}{10}\left(s\right)\)