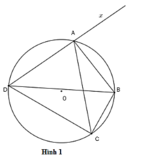
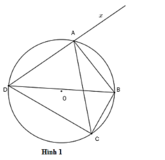
Cho tứ giác ABCD nội tiếp đường tròn (O; R) (AB < CD). Gọi P là điểm chính giữa của cung nhỏ AB; DP cắt AB tại E và cắt CB tại K; CP cắt AB tại F và cắt DA tại I.
a. Chứng minh: Tứ giác CKID nội tiếp được và IK // AB.
b. Chứng minh: AP2 = PE .PD = PF . PC
c. Chứng minh: AP là tiếp tuyến của đường tròn ngoại tiếp tam giác AED.
d. Gọi R1, R2 là các bán kính đường tròn ngoại tiếp các tam giác AED và BED.
Chứng minh:
R1+R2=\(\sqrt{4R^2-PA^2}\)



a;* ta có : P là điểm chính giữa của cung nhỏ AB
\(\Rightarrow\) cung PA = cung PB
\(\Rightarrow\) ADP = PCB (2 góc nội tiếp chắng 2 cung bằng nhau)
\(\Leftrightarrow\) IDK = ICK
xét tứ giác CKID có :
IDK = ICK (chứng minh trên)
mà IDK và ICK là 2 góc kề nhau cùng chắng cung IK của tứ giác CKID
\(\Rightarrow\) tứ giác CKID là tứ giác nội tiếp (đpcm)
* ta có : CDA = CBA (2 góc nội tiếp cùng chắng cung CA của (o))
mà CDI = CKI (2 góc nội tiếp cùng chắng cung IC của tứ giác CKID)
\(\Rightarrow\) CKI = CBA
mà CKI và CBA nằm ở vị trí đồng vị
\(\Rightarrow\) AB//IK (đpcm)
xét \(\Delta\) PAE và \(\Delta\) PDA
ta có : PAB = ADP (cung AP bằng cung PB)
góc P chung
\(\Rightarrow\) \(\Delta\) PAE đồng dạng \(\Delta\) PDA
\(\Leftrightarrow\) \(\dfrac{PA}{PD}\) = \(\dfrac{PE}{PA}\) \(\Leftrightarrow\) PA2 = PE . PD (1)
xét \(\Delta\) PAF và \(\Delta\) PCA
ta có : PAB = PCA (cung AP bằng cung PB)
góc p cung
\(\Rightarrow\)\(\Delta\) PAF đồng dạng \(\Delta\) PCA
\(\Leftrightarrow\) \(\dfrac{PA}{PC}\) = \(\dfrac{PF}{PA}\) \(\Leftrightarrow\) PA2 = PF . PC (2)
từ (1) và (2) ta có PA2 = PE . PD = PF . PC (đpcm)