FF
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
LD
5
12 tháng 6 2017
Sử dụng tính chất tam giác đồng dạng và bất đẳng thức tam giác.
Dựng điểm E sao cho tam giác BCD đồng dạng với tam giác BEA. Khi đó, theo tính chất của tam giác đồng dạng, ta có
\(\frac{BA}{EA}=\frac{BD}{CD}\)
Suy ra \(BA.CD=EA.BD\left(1\right)\)
Mặt khác, tam giác EBC và tam giác ABD cũng đồng dạng do có
\(\frac{BA}{BD}=\frac{BE}{BC}\) và góc EBC= góc ABD
Từ đó
\(\frac{EC}{BC}=\frac{AD}{BD}\)
Suy ra
\(AD.BC=EC.BD\left(2\right)\)
Cộng (1) và (2) ta suy ra
\(AB.CD+AD.BC=BD.\left(EA+EC\right)\)
Áp dụng bất đẳng thức tam giác ta suy ra \(AB.CD+AD>BC\ge AC>BD\)
Dấu bằng xảy ra khi và chỉ khi tứ giác nội tiếp trong một đường tròn và trở thành định lý Ptoleme.
13 tháng 6 2017
Lớp 8 đã học tứ giác nội tiếp đâu mà bạn đã kết luận như vậy rồi.Bạn làm theo ý tưởng trên Wikipedia cũng phải chỉ rõ cách dựng điểm E ; kết luận dấu = xảy ra khi E,C,A thẳng hàng rồi từ đó suy ra tổng 2 góc đối của tứ giác bằng 1800
A
0
15 tháng 2 2023
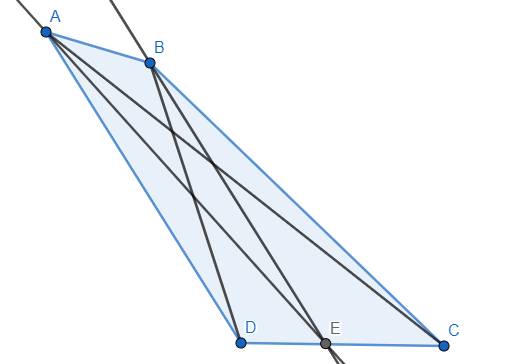
Áp dụng tính chất tia phân giác, ta có \(\dfrac{ED}{EC}=\dfrac{AD}{AC}\) và \(\dfrac{ED}{EC}=\dfrac{BD}{BC}\). Từ đó suy ra \(\dfrac{AD}{AC}=\dfrac{BD}{BC}\Rightarrow AD.BC=AC.BD\) (đpcm)
NT
Giả Sử D là 1 điểm nằm trong tam giác nhọn ABC sao cho ADB=ACB+90 và AC.BD=AD.BC> Cmr AB.CD/AC.BD=√2
1
22 tháng 2 2021
Đáp án:
nhìn dưới :3
Giải thích các bước giải:
Dựng tam giác vuông DBM cân tại B sao cho D và A nằm trên 2 nửa mặt phẳng khác nhau bờ BC ,,, suy ra tam giác ADC đồng dạng vs tam giác BMC theo c-g-c
suy ra góc BCM = góc ACD ,,, suy ra góc DCM = góc ACB và CABC=CDCMCABC=CDCM ,,,, Do đó tam giác ABC đồng dạng vs tam giác DMC theo g-c-g
Rút tỉ cạnh số ta có q.e.d
Đây là đẳng thức ptôlêmê.
C/m: Lấy 1 điểm M thuộc AC sao cho gocABD=gocMBC. Do tứ giác ABCD nội tiếp nên ^ADC=^ACB. Từ 2 điều trên suy ra tam giác ABD ~ MBC(g.g). Suy ra AD/MC=BD/BC => AD.BC=BD.MC (1)
Từ cặp tam giác đồng dạng trên ta cũng có AB/BM = BD/BC => AB/BD = BM/BC mà ^ABM = ^DBC nên tam giác ABM ~ tam giác DBC.
=> AB.CD=AM.BD (2)
Cộng (1), (2) vế theo vế suy ra AC.BD = AB . CD + AD . BC
Vậy AC.BD = AB.CD + AD . BC ( đpcm )