Trên trục số cho hai điểm c, d (h.28)

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Cac điểm –c, -d, |c|, |d| |-c|, |-d| được biểu diễn trên trục số:


Nhìn vào hệ trục tọa độ thấy d < 0 và –c < 0.
Còn lại: c, -d, |c|, |d|, |-c|, |-d| đều lớn hơn 0.

a: 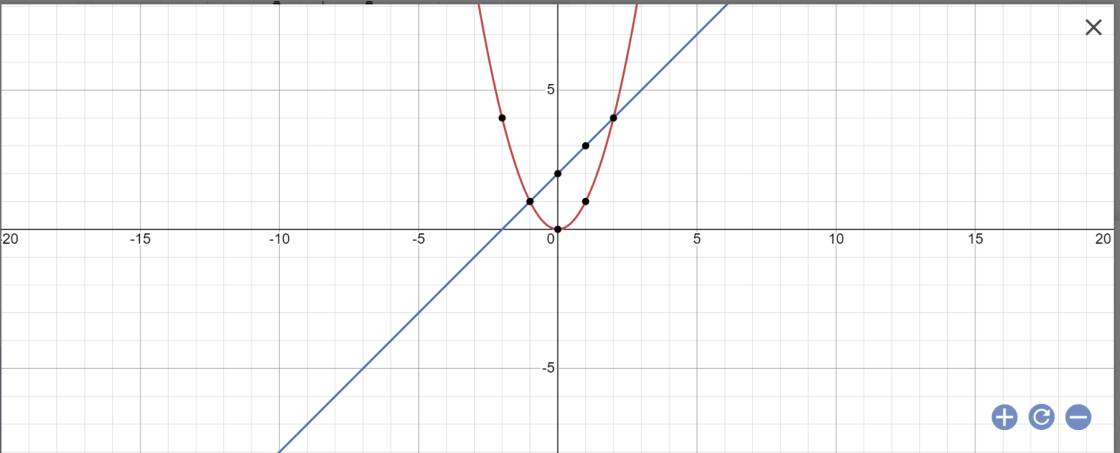
b: PTHĐGĐ là:
x^2-x-2=0
=>(x-2)(x+1)=0
=>x=2 hoặc x=-1
=>y=4 hoặc y=1
c: PTHĐGĐ là:
x^2-2x+m=0
Để (P) cắt (d1) tại hai điểm nằm về hai phía của trục tung thì m<0

a) + các điểm đặc biệt của (d):
| x | 1 | 0 |
| y | 6 | 0 |
+các điểm đặc biệt của (d1);
| x | 0 | 2 |
| y | 4 | 0 |

(hình này tớ ghi lộn tên 2 đt, đổi tên 2 đt ngược lại cho nhau nhé)
b) Gọi A, B lần lượt là giao điểm của (d1) với trục hoành, trục tung. Khi đó, A(a;0) và B(b;0)
Vì A(a;0) thuộc (d1) nên ta có (d1): \(0=4-2\cdot a\Leftrightarrow a=2\)
vậy giao điểm của (d1) và trục hoành là A(2;0)
Vì B(0;b) thuộc (d1) nên ta có (d1): \(b=4-2\cdot0=4\)
vậy giao điểm của (d1) và trục tung là B(0;4)

a) Xác định các điểm –a, -b trên trục số:

b) Xác định các điểm |a|, |b|, |-a|, |-b| trên trục số:

c) So sánh các số a, b, -a, -b, |a|, |b|, |-a|, |-b| với 0:
a ở bên trái trục số ⇒ a là số nguyên âm nên a < 0.
Do đó: -a = |-a| = |a| > 0.
b ở bên phải trục số ⇒ b là số nguyên dương nên b = |b| = |-b| > 0 và -b < 0.
Lời giải:
a) Xác định các điểm –a, -b trên trục số:
b) Xác định các điểm |a|, |b|, |-a|, |-b| trên trục số:
c) So sánh các số a, b, -a, -b, |a|, |b|, |-a|, |-b| với 0:
a ở bên trái trục số => a là số nguyên âm nên a < 0.
Do đó: -a = |a| = |a| > 0.
b ở bên phải trục số => b là số nguyên dương nên b = |b| = |-b| > 0 và -b < 0.