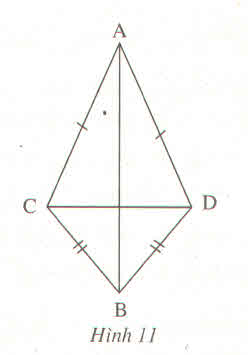
Cho hình 11. Chứng minh rằng AB vuông góc với CD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
30 tháng 9 2019
Vì AC = AD (gt) nên A thuộc đường trung trực của CD.
Vì BC = BD (gt) nên B thuộc đường trung trực của CD.
Vì A ≠ B nên AB là đường trung trực của CD.
Vậy AB ⊥ CD.
4 tháng 11 2021
a: Xét ΔAED vuông tại E và ΔBFC vuông tại F có
AD=BC
\(\widehat{D}=\widehat{C}\)
Do đó: ΔAED=ΔBFC
Suy ra: DE=FC
29 tháng 10 2017
Gọi M là trung điểm BC => BM=CM
Xét tam giác ABC có:
BM=CM
AE=EC (giả thiết vì E la trung điểm của AC)
Nên: EM là đường trung bình trong tam giác ABC
=>EM//AB và EM=AB/2
Tương tự: Xét tam giác BCD có:
FM là đường trung bình trong tam giác BCD
=>FM//CD và FM=CD/2
Lại có:
FM//CD
mà AB//CD (theo giả thiết ABCD la hthang)
Nên: FM//AB
Mà EM//AB
Do đó, theo tiên đề Ơclit ta có: E,M,F thẳng hàng.
Vậy,EF=FM-EM=(CD-AB)/2
LV
30 tháng 4 2020
Lấy M là trung điểm của CD
AC2−AD2=BC2−BD2AC2−AD2=BC2−BD2
<=> (AC−→−−AD−→−)(AC−→−+AD−→−)=(BC−→−−BD−→−)(BC−→−+BD−→−)(AC→−AD→)(AC→+AD→)=(BC→−BD→)(BC→+BD→)
<=> 2.DC−→−.AM−→−=2.DC−→−.BM−→−2.DC→.AM→=2.DC→.BM→
<=> 2.DC−→−.(AM−→−−BM−→−)=02.DC→.(AM→−BM→)=0
<=> 2.DC−→−.AB−→−=02.DC→.AB→=0
<=> DC vuông góc với AB
31 tháng 8 2023
a: Xét ΔABD và ΔBAC có
BA chung
AD=BC
BD=AC
Do đó; ΔABD=ΔBAC
=>góc OAB=góc OBA
=>OA=OB
OA+OC=AC
OB+OD=BD
mà OA=OB và AC=BD
nên OC=OD
b: Xét ΔODE vuông tại D và ΔOCE vuông tại C có
OE chung
OD=OC
Do đó; ΔODE=ΔOCE
=>ED=ED
c: Xét ΔADE và ΔBCE có
AD=BC
góc ADE=góc BCE
DE=CE
Do đó: ΔADE=ΔBCE
=>EA=EB
vì AC=AD=>A thuộc đường trung trực của CD
CB=BD=>B thuộc đường trung trực của CD
=>AB thuộc đường trung trực của CD=>AB vuông góc với CD