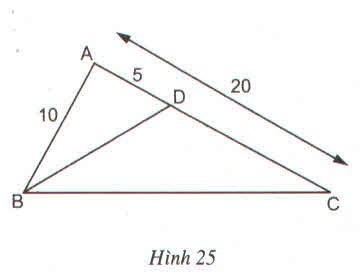
Cho tam giác ABC có AB = 10cm, AC = 20 cm. Trên cạnh AC, đặt đoạn thẳng AD = 5cm (h.25)
Chứng minh \(\widehat{ABD}=\widehat{ACB}\) ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Ta có: 
Suy ra: 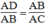
Xét △ ADB và △ ABC, ta có:
+ Góc A chung
+ 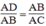 (chứng minh trên)
(chứng minh trên)
Suy ra: △ ADB đồng dạng △ ABC (c.g.c)
Vậy ∠ (ABD) = ∠ (ACB)

Xét tam giác ABD và tam giác ACB ta có ;
^BAD = ^BAC = 900
\(\frac{AB}{AC}=\frac{AD}{AB}=\frac{10}{20}=\frac{5}{10}=\frac{1}{2}\)
Vậy tam giác ABD ~ tam giác ACB ( c.g.c )
=> ^ABD = ^ACB ( 2 góc tương ứng )

Xét ΔABD và ΔACB có
AB/AC=AD/AB
góc A chung
=>ΔABD đồng dạng với ΔACB
=>góc ABD=góc ACB

\(BD=AB+AD=4+5=9\left(cm\right)\)
\(\Delta ABC\) và \(\Delta CBD\) có:
\(\frac{AB}{BC}=\frac{BC}{BD}\left(=\frac{2}{3}\right)\)
Góc B chung
\(\Rightarrow\Delta ABC\infty\Delta CBD\left(c.g.c\right)\Rightarrow\hept{\begin{cases}\widehat{ACB}=\widehat{D}\\\frac{AB}{CB}=\frac{AC}{CD}\left(1\right)\end{cases}}\)
b, Từ (1) thay số vào: \(\frac{4}{6}=\frac{5}{CD}\Rightarrow CD=7,5\left(cm\right)\)
c, \(\widehat{BAC}=\widehat{D}+\widehat{ACD}=2\widehat{D}=2\widehat{ACB}\)