Tính độ dài đường trung tuyến ứng với cạnh huyển của một tam giác vuông có các cạnh góc vuông bằng 5cm và 10 cm (làm tròn kết quả đến chữ số thập phân)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
15 tháng 5 2019
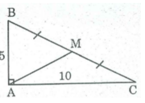
Giả sử tam giác ABC có ∠ A = 90 0 , M trung điểm BC; AB = 5cm, AC = 10cm
Áp dụng định lý Pi-ta-go vào tam giác vuông ABC, ta có:
B C 2 = A B 2 + A C 2
BC = 5 2 + 10 2 = 125 ≈ 11,2 (cm)
Mà AM = 1/2 BC (tính chất tam giác vuông)
⇒ AM = 1/2 .11,2 = 5,6 (cm)
15 tháng 5 2023
\(BC=\sqrt{5^2+12^2}=13\left(cm\right)\)
Xét ΔABC vuông tại A có sin C=AB/BC=5/13
nên góc C=22 độ
=>góc B=68 độ
AM=13/2=6,5cm
AH=5*12/13=60/13cm
21 tháng 4 2017
Bài giải:
Gọi a là độ dài cạnh huyền của tam giác vuông.
Theo định lí Pitago ta có:
a2 = 72 + 242 = 49 + 576 = 625
Nên a = 25cm
Trung tuyến ứng với cạnh huyền có độ dài bằng nửa độ dài cạnh huyền. Nên trung tuyến ứng với cạnh huyền có độ dài là 12,5cm.
12 tháng 10 2017
Gọi a là độ dài cạnh huyền của tam giác vuông.
Theo định lí Pitago ta có:
a2 = 72 + 242 = 49 + 576 = 625
Nên a = 25cm
Trung tuyến ứng với cạnh huyền có độ dài bằng nửa độ dài cạnh huyền. Nên trung tuyến ứng với cạnh huyền có độ dài là 12,5cm.
= 500
AC). Tính AD, DC, BD?
18 tháng 7 2019
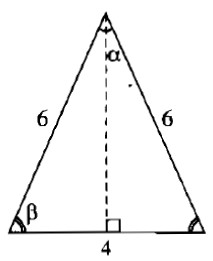
Vì các cạnh của tam giác lần lượt là 4cm, 6cm và 6cm nên tam giác đó là tam giác cân. Góc nhỏ nhất của tam giác là góc đối diện với cạnh 4cm.
Kẻ đường cao từ đỉnh của góc nhỏ nhất. Đường cao chia cạnh đáy thành hai phần bằng nhau mỗi phần 2cm.
Ta có: cosβ=26=13⇒β≈70∘32′cosβ=26=13⇒β≈70∘32′
Suy ra: α=180∘–(β+β)=180∘–2.70∘32'=38∘56′α=180∘–(β+β)=180∘–2.70∘32′=38∘56′
Vậy góc nhỏ nhất của tam giác bằng 38∘56′38∘56′.
16 tháng 5 2022
\(AH=\sqrt{25\cdot64}=40\left(cm\right)\)
Xét ΔAHB vuông tại H có
\(\tan B=\dfrac{AH}{HB}=\dfrac{40}{25}=1.6\)
nên \(\widehat{B}\simeq58^0\)
hay \(\widehat{C}=32^0\)
Theo định lý Py-ta-go ta có độ dài cạnh huyền là
\(\sqrt{5^{2} + 10^{2}}\)= \(\sqrt{25 + 100}\)= \(\sqrt{125}\)\(\approx\)11,1 (cm)
Vậy .........................
_______________ JK ~ Liên Quân Group ________________
Giả sử ∆ ABC có ˆA=900A^=900 , M trung điểm của BC; AB = 5cm; AC = 10cm. Theo định lý Pi-ta-go ta có:
\(BC^2=AB^2+AC^2\)
\(BC=\sqrt{5^2+10^2}=\sqrt{125}\approx11,2cm\)
\(AM=\dfrac{1}{2}BC\) (tính chất tam giác vuông)
⇒ \(AM\approx\dfrac{1}{2}.11,2=5,6cm\)