a) Biết rằng \(x=4\) thì hàm số \(y=3x+b\) có giá trị là 11. Tìm b. Vẽ đồ thị của hàm số với giá trị b vừa tìm được
b) Biết rằng đồ thị của hàm số \(y=ax+5\) đi qua điểm \(A\left(-1;3\right)\). Tìm a. Vẽ đồ thị của hàm số với giá trị a vừa tìm được
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
27 tháng 12 2017
a) Thay x = 4 và y = 11 vào y = 3x + b ta được:
11 = 3.4 + b = 12 + b
=> b = 11 – 12 = -1
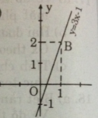
Ta được hàm số y = 3x – 1
- Cho x = 0 => y = -1 được A(0; -1)
- Cho x = 1 => y = 2 được B(1; 2).
Nối A, B ta được đồ thị hàm số y = 3x – 1.
b) Thay tọa độ điểm A(-1; 3) vào phương trình y = ax + 5 ta có:
3 = a(-1) + 5
=> a = 5 – 3 = 2
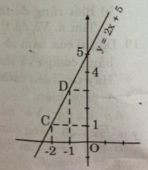
Ta được hàm số y = 2x + 5.
- Cho x = -2 => y = 1 được C(-2; 1)
- Cho x = -1 => y = 3 được D(-1; 3)
Nối C, D ta được đồ thị hàm số y = 2x + 5.
M
22 tháng 8 2023
a) Để tìm giá trị của b, ta thay x = 2 vào phương trình y = -3x + b - 3x^2 + c. Vì y = 1, ta có:
1 = -3(2) + b - 3(2)^2 + c 1 = -6 + b - 12 + c 1 = b + c - 18
Đồng thời, ta biết rằng đồ thị của hàm số đi qua điểm (2, 1), vì vậy ta có thêm một điều kiện:
1 = -3(2) + b - 3(2)^2 + c 1 = -6 + b - 12 + c 1 = b + c - 18
Từ hai phương trình trên, ta có thể giải hệ phương trình để tìm giá trị của b.
b) Để tìm a và b, ta sử dụng hai điểm A(2, 3) và B(1, 1) để lập hệ phương trình:
3 = a(2) + b(2)^2 + c 1 = a(1) + b(1)^2 + c
Từ đó, ta có thể giải hệ phương trình để tìm giá trị của a và b.
Sau khi tìm được giá trị của a và b, ta có thể vẽ đồ thị của hàm số y = ax + b + c.
18 tháng 11 2021
\(a,\Leftrightarrow1-a=\dfrac{1}{2}\Leftrightarrow a=\dfrac{1}{2}\)
Hệ số góc: \(\dfrac{1}{2}\)
\(b,a=\dfrac{1}{2}\Leftrightarrow y=\dfrac{1}{2}x+1\)
14 tháng 1 2022
Bài 9:
b: Điểm A thuộc đồ thị vì \(y_A=4=-2\cdot\left(-2\right)=-2\cdot x_A\)
Bài 10:
a: Thay x=1 và y=-3 vào (d), ta được:
\(a\cdot1=-3\)
hay a=-3
11 tháng 11 2016
em gửi bài qua fb thầy chữa cho nhé, tìm fb của thầy bằng sđt: 0975705122 nhé.
AH
Akai Haruma
Giáo viên
22 tháng 2 2021
Lời giải:
a) Vì $A$ thuộc ĐTHS nên:
$y_A=ax_A\Leftrightarrow 1=a.2\Rightarrow a=\frac{1}{2}$
b)
Với $a$ tìm được thì ĐTHS là: $y=\frac{1}{2}x$
$y(2)=\frac{1}{2}.2=1$
$y(-1)=\frac{1}{2}.(-1)=-\frac{1}{2}$
$y(2021)=\frac{1}{2}.2021=\frac{2021}{2}$
c)
Hình vẽ:
22 tháng 2 2021
a) Để đồ thị hàm số y=ax đi qua điểm A(2;1) thì
Thay x=2 và y=1 vào hàm số y=ax, ta được:
\(2a=1\)
hay \(a=\dfrac{1}{2}\)
Vậy: Để đồ thị hàm số y=ax đi qua điểm A(2;1) thì \(a=\dfrac{1}{2}\)
Bài giải:
a) Thế x = 4 và y = 11 vào y = 3x +b ta có: 11 = 3.4 + b ⇔ b = -1. Khi đó hàm số đã cho trở thành: y = 3x – 1. Đây là đường thẳng đi qua 2 điểm A(0;-1) và B(1/3; 0)
b) Đồ thị hàm số y = ax + 5 đi qua điểm A(-1; 3) nên: 3 = a(-1) + 5
<=> a = 2
Khi đó hàm số đã cho trở thành : y = 2x + 5. Đây là đường thẳng đi qua hai điểm A(0; 5) và B (−52;0)(−52;0)