Cho hình 57 :
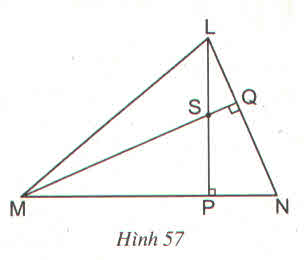
a) Chứng minh \(NS\perp LM\)
b) Khi \(\widehat{LNP}=50^0\), hãy tính góc MSP và góc PSQ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
UI
5
PT
1
CM
15 tháng 12 2018
+ Ta có : trong tam giác vuông, hai góc nhọn phụ nhau nên :
ΔNMQ vuông tại Q có:
13 tháng 4 2016
a) Chứng minh NS ⊥ LM
b) Khi =500, hãy tính góc MSP và góc PSQ
Hướng dẫn:
a) Trong ∆NML có :
LP ⊥ MN nên LP là đường cao
MQ ⊥ NL nên MQ là đường cao
mà PL ∩ MQ = {S}
suy ra S là trực tâm của tam giác nên đường thằng SN chứa đường cao từ N hay
SN ⊥ ML
b) ∆NMQ vuông tại Q có =500 nên
=400
∆MPS vuông tại Q có =400 nên
=500
Suy ra =1300(kề bù)
CM
19 tháng 5 2019
Trong ΔMNL có:
LP ⊥ MN nên LP là đường cao của ΔMNL.
MQ ⊥ NL nên MQ là đường cao của ΔMNL.
Mà LP, MQ cắt nhau tại điểm S
Nên: theo tính chất ba đường cao của một tam giác, S là trực tâm của tam giác.
⇒ đường thẳng SN là đường cao của ΔMNL.
hay SN ⊥ ML.
CT
6 tháng 5 2018
Xét tam giác MNK có
MQ vuông góc với MK
KB vuông góc với MN
MQ cắt KB tại S
=> S là trực tâm của tam giác MNK
=> NS vuông góc với MK
Ta có ^PNS + ^ PSN = ^SNQ+^NSQ = 90 độ
=> ^PNS + ^ PSN +^SNQ+^NSQ=180\(^0\)
MÀ ^PNS+^SNQ = 50 độ
=> ^PSN+^NSQ = 130 độ hay ^PSQ = 130 độ
NV
Nguyễn Việt Lâm
Giáo viên
8 tháng 5 2023
a.
\(\left\{{}\begin{matrix}SO\perp\left(ABCD\right)\Rightarrow SO\perp AC\\AC\perp BD\left(\text{hai đường chéo hình vuông}\right)\end{matrix}\right.\)
\(\Rightarrow AC\perp\left(SBD\right)\)
Mà \(AC\in\left(SAC\right)\Rightarrow\left(SAC\right)\perp\left(SBD\right)\)
b.
\(SO\perp\left(ABCD\right)\Rightarrow OC\) là hình chiếu vuông góc của SC lên (ABCD)
\(\Rightarrow\widehat{SCO}\) là góc giữa SC và (ABCD)
\(OC=\dfrac{1}{2}AC=a\sqrt{2}\)
\(tan\widehat{SCO}=\dfrac{SO}{OC}=\sqrt{3}\Rightarrow\widehat{SCO}=60^0\)
c.
Gọi E là trung điểm CD, từ O kẻ \(OF\perp SE\)
OE là đường trung bình tam giác BCD \(\Rightarrow\left\{{}\begin{matrix}OE=\dfrac{1}{2}BC=a\\OE||BC\Rightarrow OE\perp CD\end{matrix}\right.\)
\(\Rightarrow CD\perp\left(SOE\right)\)\(\Rightarrow CD\perp OF\)
\(\Rightarrow OF\perp\left(SCD\right)\Rightarrow OF=d\left(O;\left(SCD\right)\right)\)
Do \(\left\{{}\begin{matrix}AO\cap\left(SCD\right)=C\\AC=2OC\end{matrix}\right.\) \(\Rightarrow d\left(AB;\left(SCD\right)\right)=d\left(A;\left(SCD\right)\right)=2d\left(O;\left(SCD\right)\right)=2OF\)
Hệ thức lượng: \(OF=\dfrac{OE.SO}{\sqrt{OE^2+SO^2}}=...\)
27 tháng 2 2020
a, tam giác ABC cân tại A (gt)
=> góc B = (180 - góc A) : 2
góc A = 50 (gt)
=> góc B = (180 - 50) : 2
=> góc B = 65
b, xét tam giác AMB và tam giác AMC có : AB = AC do tam giác ABC cân tại A (gt)
góc ABC = góc ACB do tam giác ABC cân tại A (gT)
BM = MC do M là trđ của BC (gt)
=> tam giác AMB = tam giác AMC (c-g-c)
=> góc AMB = góc AMC (đn)
mà góc AMB + góc AMC = 180 (kb)
=> góc AMB = 90
=> AM _|_ BC (đn)
b, tam giác AMB = tam giác AMC (Câu b)
=> góc MAB = góc MAC (đn) mà AM nằm giữa AB và AC
=> AM là pg của góc BAC (đn)
HA
27 tháng 2 2020
A)VÌ \(\Delta ABC\)CÂN TẠI A
\(\Rightarrow\hept{\begin{cases}AB=AC\\\widehat{B}=\widehat{C}\end{cases}}\)
XÉT TAM GIÁC ABC
CÓ\(\widehat{A}+\widehat{B}+\widehat{C}=180^o\left(đ/l\right)\)
THAY\(50^o+\widehat{B}+\widehat{C}=180^o\)
\(\widehat{B}+\widehat{C}=130^o\)
vì\(\widehat{B}=\widehat{C}\)
THAY \(\widehat{C}+\widehat{C}=130^o\)
\(2\widehat{C}=130^o\)
\(\widehat{C}=130^o:2=65^o\)
\(\Rightarrow\widehat{B}=\widehat{C}=65^o\)
B)XÉT\(\Delta BAM\)VÀ\(\Delta CAM\)CÓ
\(BA=CA\left(GT\right)\)
\(\widehat{B}=\widehat{C}\left(GT\right)\)
\(BM=CM\left(GT\right)\)
\(\Rightarrow\Delta BAM=\Delta CAM\left(C-G-C\right)\)
\(\Rightarrow\widehat{M_1}=\widehat{M_2}\)HAI GÓC TƯƠNG ỨNG
MÀ \(\widehat{M_1}+\widehat{M_2}=180^o\left(KB\right)\)
THAY\(\widehat{M_2}+\widehat{M_2}=180^o\)
\(2\widehat{M_2}=180^o\)
\(\widehat{M_2}=180^o:2=90^o\)
VẬY \(AM\perp BC\left(đpcm\right)\)
c) \(AM\perp BC\left(cmt\right)\)
=> AM LÀ ĐƯƠNG CAO CỦA TAM GIÁC ABC
TRONG TAM GIÁC CÂN ĐƯỜNG CAO CŨNG CHÍNH LÀ ĐƯỜNG PHÁP TUYẾN,PHÂN GIÁC,TRUNG TUYẾN
=> AM LÀ PHÂN GIÁC CỦA\(\widehat{BAC}\)
a) Từ hình vẽ ta có: LP ⊥ MN; MQ ⊥ LN
ΔMNL có S là giao điểm của hai đường cao LP và MQ nên S chính là trực tâm của tam giác (định lí ba đường cao).
=> NS cũng là đường cao trong tam giác hay NS ⊥ LM (đpcm).
b) ΔNMQ vuông tại Q có góc LNP = 50o nên góc QMN = 40o
ΔMPS vuông tại P có góc QMP = 40o nên góc MSP = 50o
Vì hai góc MSP và PSQ là hai góc kề bù nên suy ra:
góc PSQ = 180o - 50o = 130o.
Hướng dẫn:
a) Trong ∆NML có :
LP ⊥ MN nên LP là đường cao
MQ ⊥ NL nên MQ là đường cao
mà PL ∩ MQ = {S}
suy ra S là trực tâm của tam giác nên đường thằng SN chứa đường cao từ N hay
SN ⊥ ML
b) ∆NMQ vuông tại Q có ˆLNPLNP^ =500 nên ˆQMNQMN^ =400
∆MPS vuông tại Q có ˆQMPQMP^ =400 nên ˆMSPMSP^ =500
Suy ra ˆPSQPSQ^ =1300(kề bù)