Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Ta có: ΔABC cân tại A
mà AI là đường phân giác
nên I là trung điểm của BC và AI\(\perp\)BC
Xét ΔMBC có
MI là đường cao
MI là đường trung tuyến
Do đó: ΔMBC cân tại M
b: Ta có: AI\(\perp\)BC
I là trung điểm của BC
Do đó: AI là đường trung trực của BC
c: Ta có: DH\(\perp\)BC
AI\(\perp\)BC
Do đó: DH//AI
=>\(\widehat{BDH}=\widehat{BAI}\)(hai góc đồng vị)
mà \(\widehat{BAC}=2\cdot\widehat{BAI}\)(AI là phân giác của góc BAC)
nên \(\widehat{BAC}=2\cdot\widehat{BDH}\)

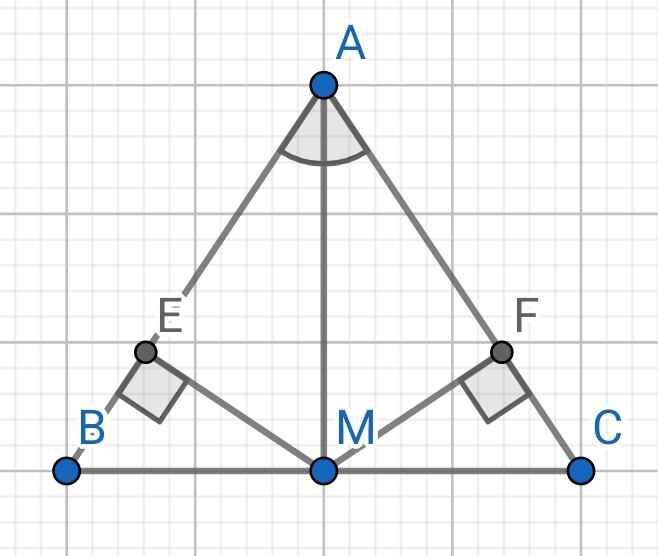 a) Do AM là tia phân giác của ∠BAC (gt)
a) Do AM là tia phân giác của ∠BAC (gt)
⇒ ∠BAM = ∠CAM
Xét ∆ABM và ∆ACM có:
AB = AC (gt)
∠BAM = ∠CAM (cmt)
AM là cạnh chung
⇒ ∆ABM = ∆ACM (c-g-c)
b) Do ∆ABM = ∆ACM (cmt)
⇒ BM = CM (hai cạnh tương ứng)
⇒ M là trung điểm của BC
Do ∆ABM = ∆ACM (cmt)
⇒ ∠AMB = ∠AMC (hai góc tương ứng)
Mà ∠AMB + ∠AMC = 180⁰ (kề bù)
⇒ ∠AMB = ∠AMC = 180⁰ : 2 = 90⁰
⇒ AM ⊥ BC
c) Do ∠BAM = ∠CAM (cmt)
⇒ ∠EAM = ∠FAM
Xét hai tam giác vuông: ∆AME và ∆AMF có:
AM là cạnh chung
∠EAM = ∠FAM (cmt)
⇒ ∆AME = ∆AMF (cạnh huyền góc nhọn)
⇒ ME = MF (hai cạnh tương ứng)
a,
Xét tam giác ABC có:
+ AB = AC (giả thuyết)
+ Góc CAM = MAB (AM là phân giác góc BAC)
+ AM chung
⇒ 2 tam giác bằng nhau (cgc) (đpcm)
b,
Ta có:
+ Tam giác AMC = Tam giác ABM (theo câu a)
⇒ CM = MB (2 cạnh tương ứng) (1)
⇒ M là trung điểm BC (đpcm)
+ Mà AM là tia phân giác góc CAB (2)
+ Góc AMC = Góc AMB (3)
Từ (1), (2), (3).
⇒ AM ⊥ BC (t/c) (đpcm)
c,
Ta có:
Tam giác ACM = Tam giác ABM (theo câu A)
⇒ Góc ACM = Góc ABM (2 góc tương ứng)
Ta có:
+ ME ⊥ AB (giả thuyết)
⇒ Tam giác MEB vuông tại E
+ MF ⊥ AC (giả thuyết)
⇒ Tam giác CFM vuông tại F
Xét tam giác CFM vuông tại F và tam giác MEB vuông tại E có:
+ Góc ACM bằng góc ABM (chứng minh trên)
+ MC = MB (theo câu b)
⇒ Hai tam giác CFM = MEB (cạnh huyền góc nhọn)
⇒ ME = MF (hai cạnh tương ứng) (đpcm)

Cho △ABC có AB = AC, AM là phân giác của ∠BAC (M ∈ BC):
a, Chứng minh △ABM = △ACM.
b, Chứng minh M là trung điểm của BC và AM ⊥ BC.
c, Kẻ MF ⊥ AB (F ∈ AB) và ME ⊥ AC (E ∈ AC). Chứng minh EF // BC.
Giải:
a,
- Xét 2 △ABM và △ACM, có:
AB = AC (theo giả thiết)
∠CAM = ∠BAM (AM là phân giác của ∠BAC)
AM_cạnh chung
=> △ABM = △ACM (c.g.c)
b,
- Có △ABM = △ACM (chứng minh trên)
=> MC = MB (2 cạnh tương ứng)
=> M là trung điểm của BC
=> ∠AMC = ∠AMB (2 góc tương ứng)
mà 2 ∠AMC và ∠AMB kề bù
=> ∠AMC = ∠AMB = \(\dfrac{180^o}{2}\) = 90o
<=> AM ⊥ BC
c,
- Xét 2 △AEM và △AFM, có:
∠AEM = ∠AFM = 90o
AM_cạnh chung
∠EAM = ∠FAM (AM là phân giác của ∠EAF)
=> △AEM = △AFM (cạnh huyền - góc nhọn)
=> AE = AF (2 cạnh tương ứng)
<=> △AEF cân tại A
=> ∠AEF = \(\dfrac{180^o-\text{∠}EAF}{2}\) (số đo của một góc ở đáy trong △AEF cân tại A) (1)
Có △ABC cân tại A (AB = AC)
=> ∠ACB = \(\dfrac{180^o-\text{∠}BAC}{2}\) (số đo của một góc ở đáy trong ΔABC cân tại A) (2)
Từ (1) và (2) suy ra ∠AEF = ∠ACB
mà ∠AEF và ∠ACB ở vị trí đồng vị
=> EF//BC

Lời giải:
a.
Do tam giác $ABC$ cân tại $A$ nên $AB=AC$
Xét tam giác $ABM$ và $ACM$ có:
$AB=AC$
$AM$ chung
$BM=CM$ (do $M$ là trung điểm $BC$)
$\Rightarrow \triangle ABM=\triangle ACM$ (c.c.c)
b.
Từ tam giác bằng nhau phần a suy ra $\widehat{BAM}=\widehat{CAM}$. Mà $AM$ nằm giữa $AB, AC$ nên $AM$ là tia phân giác $\widehat{BAC}$
Cũng từ tam giác bằng nhau phần a suy ra:
$\widehat{AMB}=\widehat{AMC}$
Mà $\widehat{AMB}+\widehat{AMC}=\widehat{BMC}=180^0$
$\Rightarrow \widehat{AMB}=180^0:2=90^0$
$\Rightarrow AM\perp BC$
c.
$AM\perp BC, M$ là trung điểm $BC$ nên $AM$ là đường trung trực của $BC$
$\Rightarrow$ mọi điểm $E\in AM$ đều cách đều 2 đầu mút B,C (theo tính chất đường trung trực)
$\Rightarrow EB=EC$
$\Rightarrow \triangle EBC$ cân tại $E$.

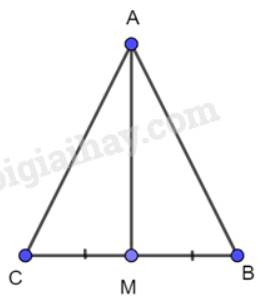
Xét 2 tam giác AMB và AMC có:
AM chung
AB=AC (do tam giác ABC cân tại A)
MB=MC (gt)
\(\Rightarrow\) \(\Delta AMB=\Delta AMC\) (c.c.c)
\(\Rightarrow\) \(\widehat {BAM} = \widehat {CAM}\)(2 góc tương ứng).
Mà tia AM nằm trong góc BAC
\(\Rightarrow\) AM là phân giác của góc BAC
Mặt khác: Do \(\Delta AMB=\Delta AMC\) nên \(\widehat {AMB} = \widehat {AMC}\)(2 góc tương ứng) mà \(\widehat {AMB} + \widehat {AMC} = {180^o}\)( 2 góc kề bù)
Nên: \(\widehat {AMB} = \widehat {AMC} = {90^o}\).
Vậy AM vuông góc với BC.
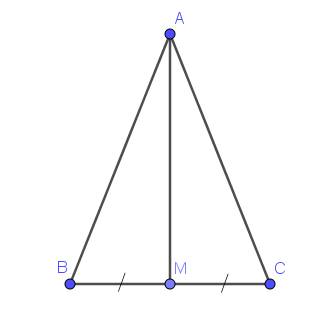


a, tam giác ABC cân tại A (gt)
=> góc B = (180 - góc A) : 2
góc A = 50 (gt)
=> góc B = (180 - 50) : 2
=> góc B = 65
b, xét tam giác AMB và tam giác AMC có : AB = AC do tam giác ABC cân tại A (gt)
góc ABC = góc ACB do tam giác ABC cân tại A (gT)
BM = MC do M là trđ của BC (gt)
=> tam giác AMB = tam giác AMC (c-g-c)
=> góc AMB = góc AMC (đn)
mà góc AMB + góc AMC = 180 (kb)
=> góc AMB = 90
=> AM _|_ BC (đn)
b, tam giác AMB = tam giác AMC (Câu b)
=> góc MAB = góc MAC (đn) mà AM nằm giữa AB và AC
=> AM là pg của góc BAC (đn)
A)VÌ \(\Delta ABC\)CÂN TẠI A
\(\Rightarrow\hept{\begin{cases}AB=AC\\\widehat{B}=\widehat{C}\end{cases}}\)
XÉT TAM GIÁC ABC
CÓ\(\widehat{A}+\widehat{B}+\widehat{C}=180^o\left(đ/l\right)\)
THAY\(50^o+\widehat{B}+\widehat{C}=180^o\)
\(\widehat{B}+\widehat{C}=130^o\)
vì\(\widehat{B}=\widehat{C}\)
THAY \(\widehat{C}+\widehat{C}=130^o\)
\(2\widehat{C}=130^o\)
\(\widehat{C}=130^o:2=65^o\)
\(\Rightarrow\widehat{B}=\widehat{C}=65^o\)
B)XÉT\(\Delta BAM\)VÀ\(\Delta CAM\)CÓ
\(BA=CA\left(GT\right)\)
\(\widehat{B}=\widehat{C}\left(GT\right)\)
\(BM=CM\left(GT\right)\)
\(\Rightarrow\Delta BAM=\Delta CAM\left(C-G-C\right)\)
\(\Rightarrow\widehat{M_1}=\widehat{M_2}\)HAI GÓC TƯƠNG ỨNG
MÀ \(\widehat{M_1}+\widehat{M_2}=180^o\left(KB\right)\)
THAY\(\widehat{M_2}+\widehat{M_2}=180^o\)
\(2\widehat{M_2}=180^o\)
\(\widehat{M_2}=180^o:2=90^o\)
VẬY \(AM\perp BC\left(đpcm\right)\)
c) \(AM\perp BC\left(cmt\right)\)
=> AM LÀ ĐƯƠNG CAO CỦA TAM GIÁC ABC
TRONG TAM GIÁC CÂN ĐƯỜNG CAO CŨNG CHÍNH LÀ ĐƯỜNG PHÁP TUYẾN,PHÂN GIÁC,TRUNG TUYẾN
=> AM LÀ PHÂN GIÁC CỦA\(\widehat{BAC}\)