Xác định các giá trị của A, B để hai mặt phẳng sau đây song song với nhau :
\(\left(\alpha\right):Ax-y+3z+2=0\)
\(\left(\beta\right):2x+By+6z+7=0\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vectơ →nn→(2 ; -1 ; 3) là vectơ pháp tuyến của mặt phẳng ( β) .
Vì (α) // ( β) nên →nn→ cũng là vectơ pháp tuyến của mặt phẳng (α) .
Phương trình mặt phẳng (α) có dạng:
2(x - 2) - (y + 1) + 3(z - 2) = 0
hay 2x - y + 3z -11 = 0.

Chọn đáp án C
Mặt phẳng (P) có vectơ pháp tuyến là n 1 ⇀ = 2 ; a ; 3 ; mặt phẳng (Q) có vectơ pháp tuyến là n 2 ⇀ = b ; - 6 ; - 6 .
Để (P)//(Q) thì n 1 ⇀ , n 2 ⇀ cùng phương hay n 1 ⇀ = k n 2 ⇀
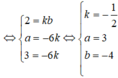
\(\left(\alpha\right)\) // \(\left(\beta\right)\) \(\Rightarrow\dfrac{A}{2}=-\dfrac{1}{B}=\dfrac{3}{6}\ne\dfrac{2}{7}\)
\(\Leftrightarrow\left\{{}\begin{matrix}A=1\\B=-2\end{matrix}\right.\)