Cho tam giác ABC. Chứng minh rằng :
a) Góc A nhọn khi và chỉ khi \(a^2< b^2+c^2\)
b) Góc A tù khi và chỉ khi \(a^2>b^2+c^2\)
c) Góc A vuông khi và chỉ khi \(a^2=b^2+c^2\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
AT
Anh Triêt
30 tháng 3 2017
Đúng(1)
Những câu hỏi liên quan
CM
3 tháng 4 2019
Trong tam giác ABC, theo Hệ quả định lý Cô sin ta luôn có :
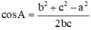
Mà ta có 2.bc > 0 nên cos A luôn cùng dấu với b2 + c2 – a2.
a) Góc A nhọn ⇔ cos A > 0 ⇔ b2 + c2 – a2 > 0 ⇔ a2 < b2 + c2.
b) Góc A tù ⇔ cos A < 0 ⇔ b2 + c2 – a2 < 0 ⇔ a2 > b2 + c2.
c) Góc A vuông ⇔ cos A = 0 ⇔ b2 + c2 – a2 = 0 ⇔ a2 = b2 + c2.
PD
17 tháng 8 2020
Theo định lý côsin ta có \(a^2=b^2+c^2-2bc.cosA\)
Khi \(a^2=b^2+c^2-bc\)thì \(2cosA=1\Rightarrow cosA=\frac{1}{2}\Rightarrow\widehat{A}=60^o\)
Khi \(a^2=b^2+c^2+bc\) thì \(-2cosA=1\Rightarrow cosA=-\frac{1}{2}\)(Khúc này để chứng minh ∠A = 120o khi và chỉ khi a 2 = b 2 + c 2 + bc. mà nó ra vầy mik chịu á , bn xem lại đề ik nha)
13 tháng 8 2017
a)Kẻ đường cao : BH , AI , CK
Ta có: sinA = BH / c ; sinB = AI / c
=> sinA/sinB = BH / AI ﴾1﴿
Mà BH = a.sinC ; AI = b.sinC
=> BH/AI = a/b ﴾2﴿
Từ ﴾1﴿ và ﴾2﴿ suy ra sinA/sinB = a/b => a/sinA = b/sinB
Bạn chỉ việc nói chứng minh tượng tự , ta có:
b/sinB = c/sinC ; c/sinC = a/sinA
Từ đó suy ra a /sinA = b / sinB = c /sinC
Chúc bạn học tốt
NHỚ TK MK NHA
PD
18 tháng 8 2020
4/Gọi hai trung tuyến kẻ từ B, C là BM và CN, chúng cắt nhau tại O
Bây giờ ta sẽ chứng minh rằng : Nếu hai trung tuyến đó vuông góc thì b^2 + c^2 = 5a^2 , từ đó suy ra điều ngược lại (vì mệnh đề này đúng với thuận và đảo)
Gỉa sử BM vuông góc với CN tại O
Ta đặt OM = x => OB = 2x và => OC =2y
AB^2/4 + AC^2/4= NB^2 + MC^2 = ON^2 + OB^2 + OM^2 + OC^2 = 5(x^2 + y^2)
=> AB^2 + AC^2 = 20(x^2 + y^2)
Mà BC^2 = OC^2 + OB^2 = 4(x^2 + y^2)
Suy ra : AB^2 + AC^2 = 5.4(x^2 + y^2) = 5BC^2 hay b^2 + c^2 = 5a^2
ta có điều ngược lại là nếu b^2 + c^2 = 5a^2 thì hai trung tuyến vuông góc(cái này tự làm ngược nha bn)
PD
18 tháng 8 2020
5
Vẽ tam giác ABC cân tại A có góc A bằng 36 độ. Và BC=1.Khi đó góc B = góc C = 72 độ.
Vẽ BD phân giác góc B , DH vuông góc AB. Đặt AH=BH=x, ta có AB=AC=2x và DC=2x-1
Cm được tam giác ABD và BCD cân => AD=BD=BC=1
cos A = cos 36 = AH/AD=x/1=x
Vì BD là đường phân giác nên AD/DC=AB/AC => \(\frac{1}{2x-1}=\frac{2x}{1}\)
=> \(4x^2-2x-1=0\Leftrightarrow\left(2x-\frac{1}{2}\right)^2-\left(\frac{\sqrt{5}}{2}\right)^2=0\)
\(\Leftrightarrow\left(2x-\frac{1}{2}-\frac{\sqrt{5}}{2}\right)\left(2x-\frac{1}{2}+\frac{\sqrt{5}}{2}\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=\frac{\sqrt{5}+1}{4}\left(N\right)\\x=\frac{1-\sqrt{5}}{4}< 0\left(L\right)\end{cases}}\)
Vậy cos 36o = (1 + √5)/4
HQ
Hà Quang Minh
Giáo viên
24 tháng 9 2023
Áp dụng định lí cosin trong tam giác ABC, ta có:
\(B{C^2} = A{B^2} + A{C^2} - 2.AB.AC.\cos A\)
Ta có: \(\widehat A = {90^o}\) (tam giác ABC vuông tại A) \( \Leftrightarrow \cos A = \cos {90^o} = 0\)
\( \Leftrightarrow B{C^2} = A{B^2} + A{C^2}\) (đpcm)
31 tháng 1 2016
1,Ta có:4(2a+3b)+(9a+5b)
=8a+12b+9a+5b
=17a+17b chia hết cho 17
Vì (2a+3b) chia hết cho 17
=>4(2a+3b) chia hết cho 17
=>9a+5b chia hết cho 17
=>đpcm
16 tháng 6 2019
Gọi hai trung tuyến kẻ từ B, C là BM và CN, chúng cắt nhau tại O
Bây giờ ta sẽ chứng minh rằng : Nếu hai trung tuyến đó vuông góc thì b^2 + c^2 = 5a^2 , từ đó suy ra điều ngược lại (vì mệnh đề này đúng với thuận và đảo)
Gỉa sử BM vuông góc với CN tại O
Ta đặt OM = x => OB = 2x và => OC =2y
AB^2/4 + AC^2/4= NB^2 + MC^2 = ON^2 + OB^2 + OM^2 + OC^2 = 5(x^2 + y^2)
=> AB^2 + AC^2 = 20(x^2 + y^2)
Mà BC^2 = OC^2 + OB^2 = 4(x^2 + y^2)
Suy ra : AB^2 + AC^2 = 5.4(x^2 + y^2) = 5BC^2 hay b^2 + c^2 = 5a^2
Vậy ta có điều ngược lại là nếu b^2 + c^2 = 5a^2 thì hai trung tuyến vuông góc