Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Trong tam giác ABC, theo Hệ quả định lý Cô sin ta luôn có :
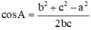
Mà ta có 2.bc > 0 nên cos A luôn cùng dấu với b2 + c2 – a2.
a) Góc A nhọn ⇔ cos A > 0 ⇔ b2 + c2 – a2 > 0 ⇔ a2 < b2 + c2.
b) Góc A tù ⇔ cos A < 0 ⇔ b2 + c2 – a2 < 0 ⇔ a2 > b2 + c2.
c) Góc A vuông ⇔ cos A = 0 ⇔ b2 + c2 – a2 = 0 ⇔ a2 = b2 + c2.

Áp dụng định lí cosin trong tam giác ABC, ta có:
\(B{C^2} = A{B^2} + A{C^2} - 2.AB.AC.\cos A\)
Ta có: \(\widehat A = {90^o}\) (tam giác ABC vuông tại A) \( \Leftrightarrow \cos A = \cos {90^o} = 0\)
\( \Leftrightarrow B{C^2} = A{B^2} + A{C^2}\) (đpcm)


Theo định lí cos ta có: \({a^2} = {b^2} + {c^2} - 2bc\;\cos A\)
\( \Rightarrow {b^2} + {c^2} - {a^2} = 2bc\;\cos A\)(1)
a) Nếu góc A nhọn thì \(\cos A > 0\)
Từ (1), suy ra \({b^2} + {c^2} > {a^2}\)
b) Nếu góc A tù thì \(\cos A < 0\)
Từ (1), suy ra \({b^2} + {c^2} < {a^2}\)
c) Nếu góc A vuông thì \(\cos A = 0\)
Từ (1), suy ra \({b^2} + {c^2} = {a^2}\)

không cần đk là a,b,c là số thực cũng được @@
Sử dụng bất đẳng thức phụ \(x^2+y^2\ge2xy\)
chứng minh : \(x^2+y^2\ge2xy< =>\left(x-y\right)^2\ge0\)*đúng*
Áp dụng vào bài toán ta được :
\(2.LHS\ge ab+bc+ca+ab+bc+ca=2\left(ab+bc+ca\right)\)
\(< =>LHS\ge ab+bc+ca\)
Dấu = xảy ra \(< =>a=b=c\)


a^2+b^2-c^2>0
=>a^2+b^2>c^2
=>a^2+b^2>a^2+b^2-2ab*cosC
=>2ab*cosC>0
=>cosC>0
=>góc C<90 độ

Mệnh đề A sai
Đúng: hai tam giác bằng nhau khi và chỉ khi chúng đồng dạng và có một cạnh tương ứng bằng nhau
