Tỉ số SABC :SABM biết M tuộc cạnh BC cùa tam giác ABC và MC=2MB
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DD
Đoàn Đức Hà
Giáo viên
22 tháng 5 2021
a) \(S_{ABM}=2S_{AMC}\)(chung đường cao hạ từ \(A\), \(BM=2CM\))
b) \(S_{ABM}=2S_{AMC}\Leftrightarrow S_{ABM}+S_{AMC}=3S_{AMC}\Leftrightarrow S_{ABC}=3S_{AMC}\Leftrightarrow S_{AMC}=\frac{S_{ABC}}{3}=3\left(cm^2\right)\)
\(S_{ABM}=2S_{AMC}=6\left(cm^2\right)\)
8 tháng 1
a:
MC+MB=BC
=>BC=2MB+MB=3MB
=>\(\dfrac{CM}{CB}=\dfrac{2MB}{3MB}=\dfrac{2}{3}\)
Xét ΔCME và ΔCBA có
\(\widehat{CME}=\widehat{CBA}\)(hai góc đồng vị, ME//AB)
\(\widehat{C}\) chung
Do đó: ΔCME đồng dạng với ΔCBA
=>\(\dfrac{CM}{CB}=\dfrac{CE}{CA}=\dfrac{ME}{BA}=\dfrac{2}{3}\)
b: ΔCME đồng dạng với ΔCBA
=>\(\dfrac{C_{CME}}{C_{CBA}}=\dfrac{CM}{CB}=\dfrac{2}{3}\)
=>\(C_{CME}=\dfrac{2}{3}\cdot24=16\left(cm^2\right)\)
CM
14 tháng 8 2017
Chọn C.
Theo định lí hàm cosin, ta có : 
Do MC = 2MB nên BM = 1/3.BC = 2.
Theo định lí hàm cosin, ta có: AM2 = AB2 + BM2 - 2AB.BM.cos B = 42 + 22 -2.4.2.1/2 = 12
Do đó: 
.
NT
3
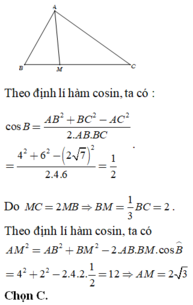
cho hình vẽ.
Ta có BM+CM=BC(vì M thuộc BC) và MC=2*BM=>3*BM=BC=>BM=1/3BC
Ta có SABC=(AH*BC)/2 hay (AH*3*BM)/2
SABM=(AH*BM)/2
=>SABC/SABM=(AH*3*BM)/2*2/(AH*BM)=(AH*3*BM)/(AH*BM)=3
Vậy SABC/SABM=3