tìm giá trị nhỏ nhất của x^2 + y^2 - 2x + 4y + 2015
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NH
1
24 tháng 12 2019
biet tong cua so thu nhat va so thu hai bang 5,8.Tong cua so thu hai va so thu ba bang 6,7.Tong so thu nhat va so thu ba bang 7,5.Tim moi so do?
NT
1
7 tháng 6 2016
\(P=8x^2+2y^2+4xy-2x+4y+2015=2\cdot\left(y^2+2xy+2y+4x^2-x\right)+2015\)
\(=2\cdot\left(y^2+2y\left(x+1\right)+\left(x+1\right)^2-\left(x+1\right)^2+4x^2-x\right)+2015\)
\(=2\cdot\left[\left(y+\left(x+1\right)\right)^2+3x^2-3x-1\right]+2015\)
\(=2\cdot\left[\left(y+x+1\right)^2+3\left(x^2-2x\cdot\frac{1}{2}+\frac{1}{4}\right)-1-\frac{3}{4}\right]+2015\)
\(=2\cdot\left[\left(y+x+1\right)^2+3\cdot\left(x-\frac{1}{2}\right)^2\right]+2015-\frac{7}{2}\)
\(=2\cdot\left(x+y+1\right)^2+6\left(x-\frac{1}{2}\right)^2+2011\frac{1}{2}\)
Vậy GTNN của P = 2011,5. Xảy ra khi x=0,5 và y=-1,5.
11 tháng 10 2019
\(A=x^2-2x+y^2-4y+6\)\(6\)
\(=x^2-2x+1+y^2-4y+4+1\)
\(=\left(x-1\right)^2+\left(y-2\right)^2+1\ge1\)
Do đó GTNN của A là 1 khi và chỉ khi:\(\hept{\begin{cases}\left(x-1\right)^2=0\\\left(y-2\right)^2=0\end{cases}}\)\(\Rightarrow\hept{\begin{cases}x=1\\y=2\end{cases}}\)
Vậy ...
S
1
HV
2
NH
13 tháng 7 2019
x2 - 2x + y2 - 4y + 7 = (x2 - 2x + 1) + ( y2 - 4y + 4) + 2 = (x - 1)2 + (y - 2)2 + 2
Vì (x - 1)2 ≥ 0 \(\forall\)x
(y - 2)2 ≥ 0 \(\forall\)x
=> (x - 1)2 + (y - 2)2 ≥ 0 \(\forall\)x
=> (x - 1)2 + (y - 2)2 + 2 ≥ 2
Dấu " = " xảy ra <=> \(\hept{\begin{cases}\left(x-1\right)^2=0\\\left(y-2\right)^2=0\end{cases}\Leftrightarrow}\hept{\begin{cases}x-1=0\\y-2=0\end{cases}\Leftrightarrow}\hept{\begin{cases}x=1\\y=2\end{cases}}\)
Vậy GTNN của x2 - 2x + y2 - 4y +7 = 2 khi x = 1; y = 2
NN
5 tháng 9 2020
Đặt \(A=x^2-2x+y^2-4y+7\)
\(\Rightarrow A=\left(x^2-2x+1\right)+\left(y^2-4y+4\right)+2\)
\(=\left(x-1\right)^2+\left(y-2\right)^2+2\)
Vì \(\left(x-1\right)^2\ge0\forall x\); \(\left(y-2\right)^2\ge0\forall y\)
\(\Rightarrow\left(x-1\right)^2+\left(y-2\right)^2\ge0\forall x,y\)
\(\Rightarrow\left(x-1\right)^2+\left(y-2\right)^2+2\ge2\forall x,y\)
hay \(A\ge2\)
Dấu " = " xảy ra \(\Leftrightarrow\hept{\begin{cases}x-1=0\\y-2=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=1\\y=2\end{cases}}\)
Vậy \(minA=2\)\(\Leftrightarrow\hept{\begin{cases}x=1\\y=2\end{cases}}\)
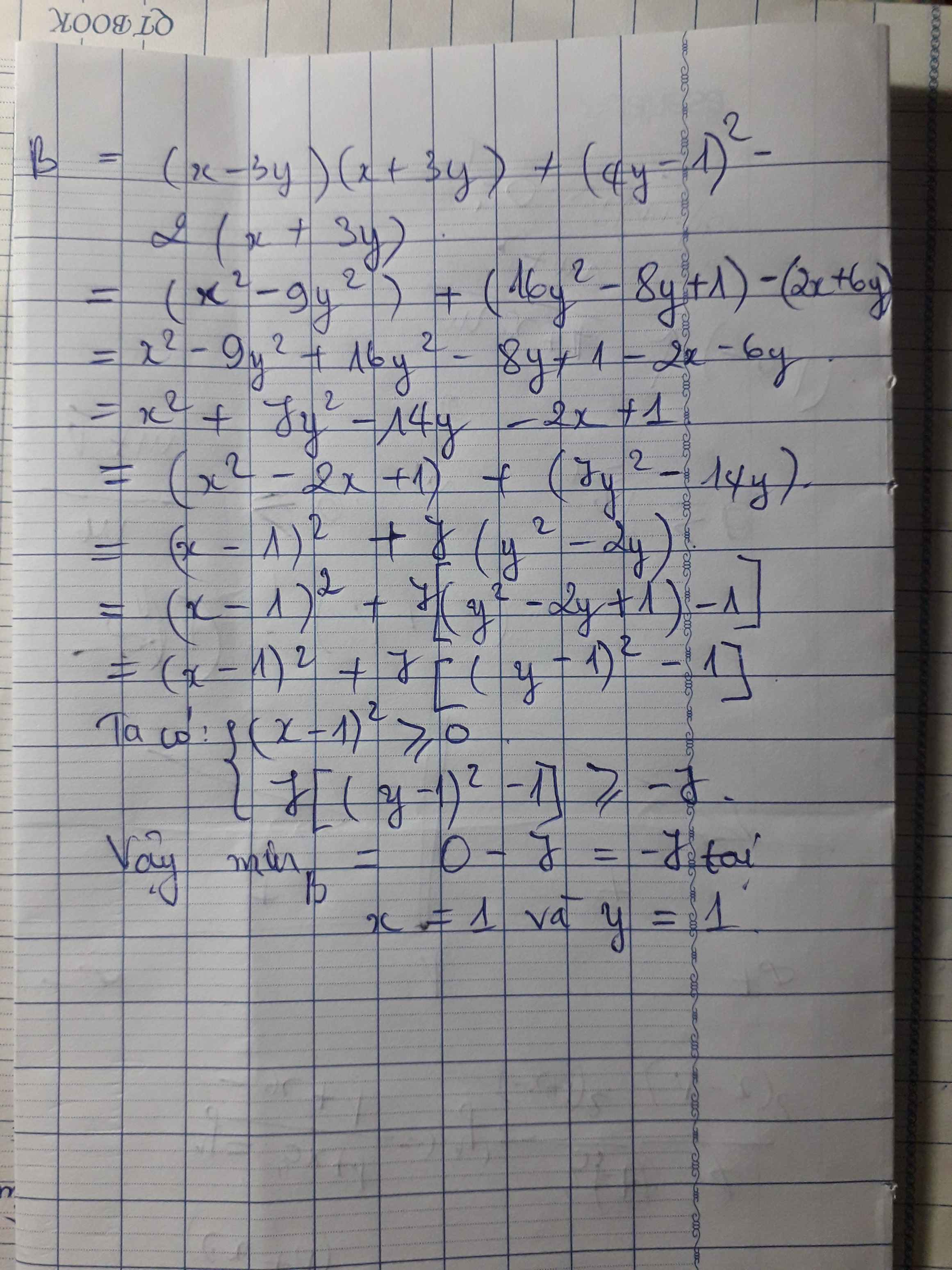
Lời giải:
$A=x^2+y^2-2x+4y+2015$
$A=(x^2-2x+1)+(y^2+4y+4)+2010$
$=(x-1)^2+(y+2)^2+2010\geq 2010$
$\Rightarrow A_{\min}=2010$
Giá trị này đạt tại $x-1=y+2=0$
$\Leftrightarrow x=1; y=-2$