Bài tập : Cho tam giác ABC, D là trung điểm của AB, E là trung điểm của AC. Vẽ điểm F sao cho E là trung điểm của DF. Chứng minh rằng :
a. DB = CF
b. ΔBDC = ΔFCD
c. DE // BC và DE = 1/2 BC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CT
15 tháng 1 2019
em xét tam giác DEA và tam giác FEC
2 tam giác đó bằng nhau
suy ra AD=CF
mà AD=DB
suy ra CF=BD
4 tháng 3 2018
Xet ∆AED=∆CEF ( c-g-c )
=) AD=CF
Mà AD=DB
Suy ra DB=CF
b+c)
Ta có D là tđ AB
F là tđ AC
Suy ra * DE//BC
=) FDC = DCB ( slt )
* DE = 1/2BC =) BC = DF
Xét∆BDC=∆FCD ( c-g-c)
T3
3 tháng 4 2020
Cho tam giác abc có gốc a bằng 90° trên bc lấy e sao cho BE = BA tia ph . Giác của góc b cắt ac ở d
a chứng minh tam giác ABD = EBD
b tính số đo BEM
c Chứng minh BD vuông góc với AE
20 tháng 12 2021
\(a,\left\{{}\begin{matrix}AE=EC\\DE=EF\\\widehat{AED}=\widehat{CEF}\left(đđ\right)\end{matrix}\right.\Rightarrow\Delta ADE=\Delta CFE\left(c.g.c\right)\\ b,\Delta ADE=\Delta CFE\\ \Rightarrow AD=CF\\ \text{Mà }AD=DB\Rightarrow BD=CF\\ c,\Delta ADE=\Delta CFE\Rightarrow\widehat{ADE}=\widehat{CFE}\\ \text{Mà 2 góc này ở vị trí slt }\Rightarrow AB\text{//}CF\)
20 tháng 12 2021
c: Xét tứ giác ADCF có
E là trung điểm của AC
E là trung điểm của DF
Do đó: ADCF là hình bình hành
Suy ra: AD//CF
hay AB//CF
23 tháng 3 2018
a) xét tam giác ADE và tam giác FEC, ta có:
+) AE = EC (E là trung điểm của AC)
+) DE = EF (E là trung điểm của DF)
\(\widehat{ADE}=\widehat{CEF}\)(hai góc đối đỉnh)
=> \(\Delta ADE=\Delta FEC\) (c = g = c)
=> AD = CF (2 cạnh tương ứng)
mà AD = DB (D là trung điểm của AB)
nên: CF = BD
b) ta có:
\(\widehat{EAD}=\widehat{ECF}\left(\Delta ADE=\Delta FEC\right)\)
mà góc EAD và góc ECF nằm so le
nên AD//CF hay AB//CF
xét tam giác BDC và tam giác DCF, ta có:
BD = CF (Cm a)
DC = DC
\(\widehat{BDC}=\widehat{FCD}\)(2 góc so le trong và AB//CF)
=> \(\Delta BDC=\Delta DCF\)(c = g = c)
c) ta có:
\(DE=\frac{1}{2}DF\)(E là trung điểm DF)
DF = BC \(\left(\Delta FCD=\Delta BDC\right)\)
=> \(DE=\frac{1}{2}BC\)
CM
10 tháng 6 2017
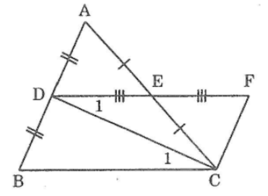
Ta có: ΔBDC= ΔFCD(chứng minh trên)
Suy ra: ∠(C1 ) =∠(D1 ) (hai góc tương ứng)
Suy ra: DE // BC ( vì có hai góc so le trong bằng nhau)
ΔBDC= ΔFCD suy ra BC = DF (hai cạnh tương ứng)
Mà DE = 1/2 DF(gt). Vậy DE = 1/2 BC
hình, bn tự vẽ nhé!
Giải:
a/ Xét t/g ADE và t/g CFE có:
AE = CE (gt)
\(\widehat{AED}=\widehat{CEF}\) (ddoois ddinhr)
DE = FE (gt)
=> t/g ADE = t/g CFE (c.g.c)
=> AD = CF
mà DB = AD (gt)
=> DB = CF (đpcm)
b/ Ta có: t/g ADE = t/g CFE (ý a)
=> \(\widehat{DAE}=\widehat{FCE}\) (2 góc tương ứng)
mà 2 góc này so le trong
=> AB // CF
=> \(\widehat{BDC}=\widehat{FCD}\) (so le trong)
\(\widehat{BCD}=\widehat{FDC}\) (so le trong)
Xét t/g BDC và t/g FCD có:
\(\widehat{BDC}=\widehat{FCD}\left(cmt\right)\)
CD : cạnh chung
\(\widehat{BCD}=\widehat{FDC}\left(cmt\right)\)
=> t/g BDC = t/g FCD (g.c.g)(đpcm)
c/ Ta có: \(\widehat{BCD}=\widehat{FDC}\) (đã cm)
mà 2 góc này ở vị trí so le trong
=> DE // BC (đpcm)
Vì t/g BDC = t/g FCD (ý b)
=> BC = FD
mà DE = EF = \(\frac{1}{2}\) FD
=> DE = EF = \(\frac{1}{2}BC\)
=> DE = \(\frac{1}{2}BC\left(đpcm\right)\)
Bạn vào trang web /hoi-dap/question/158621.html