Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔAED và ΔCEF có
EA=EC
\(\widehat{AED}=\widehat{CEF}\)
ED=EF
Do đó: ΔAED=ΔCEF
b: Xét ΔABC có
D là trung điểm của AB
E là trung điểm của AC
Do đó: DE là đường trung bình
=>DE//BC và DE=1/2BC

a) Xét ΔAND và ΔCNB có
NA=NC(N là trung điểm của AC)
\(\widehat{AND}=\widehat{CNB}\)(hai góc đối đỉnh)
ND=NB(N là trung điểm của BD)
Do đó: ΔAND=ΔCNB(c-g-c)
b) Ta có: ΔAND=ΔCNB(cmt)
nên AD=BC(hai cạnh tương ứng)
Ta có: ΔAND=ΔCNB(cmt)
nên \(\widehat{ADN}=\widehat{CBN}\)(hai góc tương ứng)
mà \(\widehat{ADN}\) và \(\widehat{CBN}\) là hai góc ở vị trí so le trong
nên AD//BC(Dấu hiệu nhận biết hai đường thẳng song song)

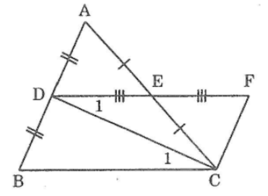
Ta có: ΔBDC= ΔFCD(chứng minh trên)
Suy ra: ∠(C1 ) =∠(D1 ) (hai góc tương ứng)
Suy ra: DE // BC ( vì có hai góc so le trong bằng nhau)
ΔBDC= ΔFCD suy ra BC = DF (hai cạnh tương ứng)
Mà DE = 1/2 DF(gt). Vậy DE = 1/2 BC

a) xét tam giác ADE và tam giác FEC, ta có:
+) AE = EC (E là trung điểm của AC)
+) DE = EF (E là trung điểm của DF)
\(\widehat{ADE}=\widehat{CEF}\)(hai góc đối đỉnh)
=> \(\Delta ADE=\Delta FEC\) (c = g = c)
=> AD = CF (2 cạnh tương ứng)
mà AD = DB (D là trung điểm của AB)
nên: CF = BD
b) ta có:
\(\widehat{EAD}=\widehat{ECF}\left(\Delta ADE=\Delta FEC\right)\)
mà góc EAD và góc ECF nằm so le
nên AD//CF hay AB//CF
xét tam giác BDC và tam giác DCF, ta có:
BD = CF (Cm a)
DC = DC
\(\widehat{BDC}=\widehat{FCD}\)(2 góc so le trong và AB//CF)
=> \(\Delta BDC=\Delta DCF\)(c = g = c)
c) ta có:
\(DE=\frac{1}{2}DF\)(E là trung điểm DF)
DF = BC \(\left(\Delta FCD=\Delta BDC\right)\)
=> \(DE=\frac{1}{2}BC\)
kk