Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
ΔBEA= ΔCDA (chứng minh trên)
⇒∠(B1 ) =∠(C1 ) ;∠(E1 ) =∠(D1 ) (hai góc tương ứng) (1)
+) Ta có: ∠(E1 ) +∠(E2 ) =180o (hai góc kề bù) (2)
Và ∠(D1 ) +∠(D2 ) =180o (hai góc kề bù) (3)
Từ (1); (2) và (3) suy ra: ∠(E2 ) =∠(D2 )
+) Theo giả thiết ta có; AB = AC
Và AD = AE
Lấy vế trừ vế, suy ra:
AB - AD = AC - AE hay BD = CE
Xét ΔOEC và ΔOCE, ta có:
∠(D2 ) =∠(E2 ) (chứng minh trên)
DB=EC (chứng minh trên)
∠(B1 ) =∠(C1 ) (chứng minh trên)
Suy ra: ΔODB= ΔOCE ( g.c.g)
a: Xét ΔABE và ΔACD có
AB=AC
\(\stackrel\frown{A}\) chung
AE=AD
Do đó: ΔABE=ΔACD
Suy ra: BE=CD
AB = AC (gt)
=> Tam giác ABC cân tại A
Xét tam giác EAB và tam giác DAC có:
EA = DA (gt)
A chung
AB = AC (gt)
=> Tam giác EAB = Tam giác DAC (c.g.c)
=> EB = DC (2 cạnh tương ứng)
EBA = DCA (2 góc tương ứng)
mà ABC = ACB (tam giác ABC cân tại A)
=> ABC - EBA = ACB - DCA
hay EBC = DCB
=> Tam giác OBC cân tại O
Xét tam giác BOD và tam giác COE có:
DBO = ECO (tam giác EAB = tam giác DAC)
BO = CO (tam giác OBC cân tại O)
BOD = COE (2 góc đối đỉnh)
=> Tam giác BOD = Tam giác COE (c.g.c)
a) Xét ∆BEA và ∆CDA, ta có:
BA = CA (gt)
\(\widehat{A}\)chung
AE = AD (gt)
Suy ra: ∆BEA = ∆CDA (c.g.c)
Vậy BE = CD (hai cạnh tương ứng)
b) ∆BEA = ∆CDA (chứng minh trên)
⇒\(\widehat{\text{B1}}=\widehat{\text{C1}}\);\(\widehat{\text{E1}}=\widehat{\text{D1}}\) (hai góc tương ứng)
\(\widehat{\text{E1}}+\widehat{\text{E2}}\)=180o (hai góc kề bù)
\(\widehat{\text{D1}}+\widehat{\text{D2}}\)=180o (hai góc kề bù)
Suy ra: \(\widehat{\text{E2}}=\widehat{\text{D2}}\)
AB = AC (gt)
⇒ AE + EC = AD + DB mà AE = AD (gt) => EC = DB
Xét ∆ODB và ∆OCE, ta có:
\(\widehat{\text{E2}}=\widehat{\text{D2}}\) (chứng minh trên)
DB = EC (chứng minh trên)
\(\widehat{\text{B1}}=\widehat{\text{C1}}\)(chứng minh trên)
Suy ra: ∆ODB = ∆OEC (g.c.g)
Cm: a) Xét t/giác ABE và t/giác ACD
có: AB = AC (gt)
\(\widehat{A}\) :chung
AE = AD (gt)
=> t/giác ABE = t/giác ACD (c.g.c)
=> BE = CD (2 cạnh t/ứng)
b)Ta có: AD + DB = AB
AE + EC = AC
mà AD = AE (gt) ; AB = AC (gt)
=> BD = EC
Ta lại có: \(\widehat{ADC}+\widehat{CDB}=180^0\) (kề bù)
\(\widehat{AEB}+\widehat{BEC}=180^0\)(kề bù)
mà \(\widehat{ADC}=\widehat{AEB}\)(vì t/giác ABE = t/giác ACD)
=> \(\widehat{BDC}=\widehat{BEC}\)
Xét t/giác BOD và t/giác COE
có: \(\widehat{DBO}=\widehat{OCE}\) (vì t/giác ABE = t/giác ACD)
BD = EC (cmt)
\(\widehat{BDO}=\widehat{OEC}\) (cmt)
=> t/giác BOD = t/giác COE (g.c.g)
c) Xét t/giác ABO và t/giác ACO
có: AB = AC (gT)
OB = OC (vì t/giác BOD = t/giác COE)
AO : chung
=> t/giác ABO = t/giác ACO (c.c.c)
=> \(\widehat{BAO}=\widehat{CAO}\) (2 góc t/ứng)
=> AO là tia p/giác của \(\widehat{A}\)
d) Xét t/giác ABH và t/giác ACH
có: AB = AC (gt)
\(\widehat{BAH}=\widehat{CAH}\)(cmt)
AH : chung
=> t/giác ABH = t/giác ACH (c.g.c)
=> \(\widehat{BHA}=\widehat{CHA}\) (2 góc t/ứng)
Mà \(\widehat{BHA}+\widehat{CHA}=180^0\) (kề bù)
=> \(\widehat{BHA}=\widehat{CHA}=90^0\) => AH \(\perp\)BC (Đpcm)
a: Xét ΔAEB và ΔADC có
AE=AD
\(\widehat{DAC}\) chung
AB=AC
Do đó: ΔAEB=ΔADC
Suy ra: BE=CF
b: Ta có: AD+DB=AB
AE+EC=AC
mà AD=AE
và AB=AC
nên DB=EC
Xét ΔDBC và ΔECB có
DB=EC
\(\widehat{DBC}=\widehat{ECB}\)
BC chung
Do đó: ΔDBC=ΔECB
Suy ra: \(\widehat{ODB}=\widehat{OEC}\)
Xét ΔODB và ΔOEC có
\(\widehat{ODB}=\widehat{OEC}\)
BD=EC
\(\widehat{DBO}=\widehat{ECO}\)
Do đó: ΔODB=ΔOEC
a/ Xét tam giác AEB và tam giác ADC có:
Góc A: chung
AD=AE(gt)
AB=AC(gt)
=> Tam giác AEB=tam giác ADC(c-g-c)
=> BE=DC(Cạnh tương ứng)
b/ Ta có: Góc DOB+ODB+OBD=180 độ
Góc OEC+EOC+ECO=180 độ
Mà Góc DOB=EOC(đối đỉnh)
Và Góc OBD=OCE(góc tương ứng)
=> Góc ODB=OEC
Ta lại có:
AB=AC(gt)
AD=AE(gt)
Mà BD=AB-AD
CE=AC-AE
=> BD=CE
Xét tam giác BOD và tam giác COD có:
BD=CE(cmt)
Góc ODB=OEC(cmt)
Góc OBD=OCE(góc tương ứng)
=> Tam giác BOC=tam giác COD(g-c-g)(đpcm)
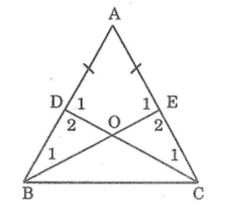
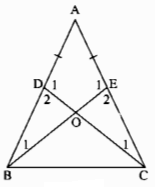
Ta có hình vẽ sau:
a/ Ta có:
AD + DB = AB
AE + EC = AC
mà AB = AC (gt) ; AE = AD (gt)
=> DB = EC
Vì AB = AC => \(\Delta ABC\) cân
=> \(\widehat{AB}C=\widehat{ACB}\)
Xét \(\Delta BEC\) và \(\Delta CDB\) có:
BC : Cạnh chung
\(\widehat{ABC}=\widehat{ACB}\left(cmt\right)\)
EC = DB (cmt)
=> \(\Delta BEC=\Delta CDB\left(c-g-c\right)\)
=> BE = CD (2 cạnh tương ứng) (đpcm)
b/ Vì \(\Delta BEC=\Delta CDB\) (ý a)
=> \(\widehat{EBC}=\widehat{DCB}\) (2 cạnh tương ứng)
mà \(\widehat{EBC}+\widehat{DBE}=\widehat{ABC}\) (2 góc kề nhau)
\(\widehat{DCB}+\widehat{ECD}=\widehat{ACB}\) (2 góc kề nhau)
ta lại có: \(\widehat{ABC}=\widehat{ACB}\) (đã cm)
=> \(\widehat{DBE}=\widehat{ECD}\)
Xét \(\Delta BOD\) và \(\Delta COE\) có:
\(\widehat{BDC}=\widehat{CEB}\) (2góc tương ứng do \(\Delta BEC=\Delta CDB\) )
DB = EC (đã cm)
\(\widehat{DBE}=\widehat{ECD}\left(cmt\right)\)
=> \(\Delta BOD=\Delta COE\left(g-c-g\right)\left(đpcm\right)\)
c/ Vì \(\Delta BOD=\Delta COE\) (ý b)
=> OD = OE (2 cạnh tương ứng)
Xét \(\Delta AOD\) và \(\Delta AOE\) có:
AO: Cạnh chung
AD = AE (gt)
OD = OE (cmt)
=> \(\Delta AOD=\Delta AOE\left(c-c-c\right)\)
\(\Rightarrow\widehat{DAO}=\widehat{EAO}\) (2 góc tương ứng)
=> AO là tia phân giác của \(\widehat{BAC}\) (đpcm)
Giải:
a) Vì \(\Delta ABC\) có AB = AC nên \(\Delta ABC\) cân tại A
\(\Rightarrow\widehat{B}=\widehat{C}\)
Ta có: AB = AC ( gt )
AD = AE ( gt )
\(\Rightarrow AB-AD=AC-AE\)
\(\Rightarrow BD=CE\)
Xét \(\Delta DBC,\Delta ECB\) có:
\(BD=CE\left(cmt\right)\)
\(\widehat{B}=\widehat{C}\left(cmt\right)\)
BC: cạnh chung
\(\Rightarrow\Delta DBC=\Delta ECB\left(c-g-c\right)\)
\(\Rightarrow BE=CD\) ( cạnh t/ứng ) ( đpcm )
\(\Rightarrow\widehat{D_1}=\widehat{E_1}\) ( góc t/ứng )
b) Ta có: \(\widehat{D_1}+\widehat{O_1}+\widehat{B_1}=180^o\) ( 3 góc của \(\Delta DOB\) )
\(\widehat{E_1}+\widehat{O_2}+\widehat{C_1}=180^o\) ( 3 góc của \(\Delta EOC\) )
Vì \(\widehat{D_1}=\widehat{E_1}\) ( theo phần a ); \(\widehat{O_1}=\widehat{O_2}\) ( đối đỉnh )
\(\Rightarrow\widehat{B_1}=\widehat{C_1}\)
Xét \(\Delta BOD,\Delta COE\) có:
\(\widehat{D_1}=\widehat{E_1}\) ( theo phần a )
\(BD=CE\) ( theo phần a )
\(\widehat{B_1}=\widehat{C_1}\left(cmt\right)\)
\(\Rightarrow\Delta BOD=\Delta COE\left(g-c-g\right)\) ( đpcm )
\(\Rightarrow OB=OC\) ( cạnh t/ứng )
c) Xét \(\Delta ABO,\Delta ACO\) có:
\(AB=AC\left(gt\right)\)
\(\widehat{B_1}=\widehat{C_1}\) ( theo phần b )
\(OB=OC\) ( theo phần b )
\(\Rightarrow\Delta ABO=\Delta ACO\left(c-g-c\right)\)
\(\Rightarrow\widehat{A_1}=\widehat{A_2}\) ( góc t/ứng )
\(\Rightarrow\)AO là tia phân giác của \(\widehat{BAC}\) ( đpcm )