(1-3x)+(x-3)=(5x-1)-(5x+3)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: \(=2x^3:\dfrac{-3}{2}x+4x:\dfrac{3}{2}x-5:\dfrac{3}{2}\)
=-4/3x^2+8/3-10/3
=-4/3x^2-2/3
d: \(\dfrac{3x^3-5x+2}{x-3}=\dfrac{3x^3-9x^2+9x^2-27x+22x-66+68}{x-3}\)
\(=3x^2+9x+22+\dfrac{68}{x-3}\)

a, \(-4x+5+2x-1=3\Leftrightarrow-2x=-1\Leftrightarrow x=\dfrac{1}{2}\)
b, \(-2x+2=2\Leftrightarrow x=0\)
c, \(-2x-6=-8\Leftrightarrow x=1\)

\(a,-5x\left(x-3\right)\left(2x+4\right)-\left(x+3\right)\left(x-3\right)+\left(5x-2\right)\left(3x+4\right)\)
\(=-5x\left(2x^2-x-12\right)-\left(x^2-9\right)+15x^2+20x-6x-8\)
\(=-10x^3+5x^2+60x-x^2+9+15x^2+20x-6x-8\)
\(=-10x^3+19x^2+74x+1\)
\(b,\left(4x-1\right)x\left(3x+1\right)-5x^2.x\left(x-3\right)-\left(x-4\right)x\left(x-5\right)\)\(-7\left(x^3-2x^2+x-1\right)\)
\(=\left(4x^2-x\right)\left(3x+1\right)-5x^4-15x^3-\left(x^2-4x\right)\left(x-5\right)\)\(-7x^3+14x^2-7x+7\)
\(=12x^3+x^2-x-5x^4-15x^3-x^3+9x^2+20x\)\(-7x^3+14x^2-7x+7\)
\(=-5x^4-11x^3+24x^2+12x+7\)
\(c,\left(5x-7\right)\left(x-9\right)-\left(3-x\right)\left(2-5x\right)-2x\left(x-4\right)\)
\(=5x^2-52x+63-6+17x-5x^2-2x^2+8x\)
\(=-2x^2-27x+57\)
\(d,\left(5x-4\right)\left(x+5\right)-\left(x+1\right)\left(x^2-6\right)-5x+19\)
\(=5x^2+21x-20-x^3-x^2+6x+6-5x+19\)
\(=-x^3+4x^2+22x+5\)
\(e,\left(9x^2-5\right)\left(x-3\right)-3x^2\left(3x+9\right)-\left(x-5\right)\left(x+4\right)-9x^3\)
\(=9x^3-27x^2-5x+15-9x^3-27x^2-x^2+x+20-9x^3\)
\(=-9x^3-55x^2+4x+35\)
\(g,\left(x-1\right)^2-\left(x+2\right)^2\)
\(=x^2-2x+1-x^2-4x-4\)
\(=-6x-3\)

a: =>|5x-2|=|2x-3|
=>5x-2=2x-3 hoặc 5x-2=-2x+3
=>3x=-1 hoặc 7x=5
=>x=5/7 hoặc x=-1/3
b: =>|5x-2|-|2x+2|=3x+5
TH1 x<-1
PT sẽ là 2-5x+2x+2=3x+5
=>-3x+4=3x+5
=>-6x=1
=>x=-1/6(loại)
TH2: -1<=x<2/5
Pt sẽ là 2-5x-2x-2=3x+5
=>-7x=3x+5
=>-4x=5
=>x=-5/4(loại)
Th3: x>=2/5
PT sẽ là 5x-2-2x-2=3x+5
=>3x-4=3x+5
=>0x=9(loại)

+) (5x-1). (2x+3)-3. (3x-1)=0
10x^2+15x-2x-3 - 9x+3=0
10x^2 +8x=0
2x(5x+4)=0
=> x=0 hoặc x= -4/5
+) x^3 (2x-3)-x^2 (4x^2-6x+2)=0
2x^4 -3x^3 -4x^4 + 6x^3 - 2x^2=0
-2x^4 + 3x^3-2x^2=0
x^2(-2x^2+x-2)=0
-2x^2(x-1)^2=0
=> x=0 hoặc x=1
+) x (x-1)-x^2+2x=5
x^2 -x -x^2+2x=5
x=5
+) 8 (x-2)-2 (3x-4)=25
8x - 16-6x+8=25
2x=33
x=33/2

a. (x−1)(5x+3)=(3x−8)(x−1)(x−1)(5x+3)=(3x−8)(x−1)
⇔(x−1)(5x+3)−(3x−8)(x−1)=0⇔(x−1)[(5x+3)−(3x−8)]=0⇔(x−1)(5x+3−3x+8)=0⇔(x−1)(2x+11)=0⇔(x−1)(5x+3)−(3x−8)(x−1)=0⇔(x−1)[(5x+3)−(3x−8)]=0⇔(x−1)(5x+3−3x+8)=0⇔(x−1)(2x+11)=0
⇔x−1=0⇔x−1=0hoặc 2x+11=02x+11=0
+ x−1=0⇔x=1x−1=0⇔x=1
+ 2x+11=0⇔x=−5,52x+11=0⇔x=−5,5
Phương trình có nghiệm x = 1 hoặc x = -5,5
b. 3x(25x+15)−35(5x+3)=03x(25x+15)−35(5x+3)=0
⇔15x(5x+3)−35(5x+3)=0⇔(15x−35)(5x+3)=0⇔15x(5x+3)−35(5x+3)=0⇔(15x−35)(5x+3)=0
⇔15x−35=0⇔15x−35=0 hoặc 5x+3=05x+3=0
+ 15x−35=0⇔x=3515=7315x−35=0⇔x=3515=\(\frac{7}{3}\)
+ 5x+3=0⇔x=−355x+3=0⇔x=−\(\frac{3}{5}\)
Phương trình có nghiệm x=\(\frac{7}{3}\)x=\(\frac{7}{3}\) hoặc x=−\(\frac{3}{5}\)

a)\(f\left(x\right)=\left(3x+4\right)\cdot\left(5x-1\right)+\left(5x+2\right)\cdot\left(1-3x\right)+2\)
\(=15x^2-3x+20x-4+5x-15x^2+2-6x+2\)
\(=16x\)
b)\(g\left(x\right)=\left(5x-1\right)\cdot\left(2x+3\right)-3\cdot\left(3x-1\right)\)
\(=10x^2+15x-2x-3-9x+3\)
\(=10x^2+4x\)

b) PT \(\Leftrightarrow15x\left(5x+3\right)-35\left(5x+3\right)=0\)
\(\Leftrightarrow\left(15x-35\right)\left(5x+3\right)=0\) \(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{7}{3}\\x=-\dfrac{3}{5}\end{matrix}\right.\)
Vậy \(S=\left\{-\dfrac{3}{5};\dfrac{7}{3}\right\}\)
c) PT \(\Leftrightarrow\left(2-3x\right)\left(x-11\right)+\left(2-3x\right)\left(2-5x\right)=0\)
\(\Leftrightarrow\left(2-3x\right)\left(-9-4x\right)=0\) \(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{2}{3}\\x=-\dfrac{9}{4}\end{matrix}\right.\)
Vậy \(S=\left\{\dfrac{2}{3};-\dfrac{9}{4}\right\}\)
a)(x-1)(5x+3)=(3x-8)(x-1)
\(\Leftrightarrow\)(x-1)(5x+3)-(3x-8)(x-1)=0
\(\Leftrightarrow\left(x-1\right)\left(5x-3-3x+8\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(2x-5\right)=0\)
\(\left[{}\begin{matrix}x-1=0\\2x-5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{5}{2}\end{matrix}\right.\)
Vậy \(x\in\left\{1;\dfrac{5}{2}\right\}\)
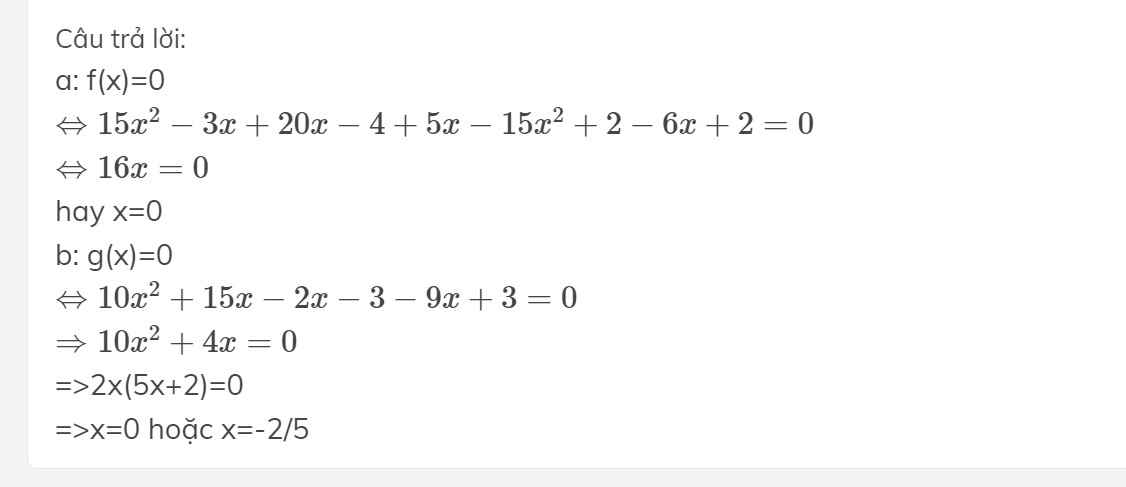
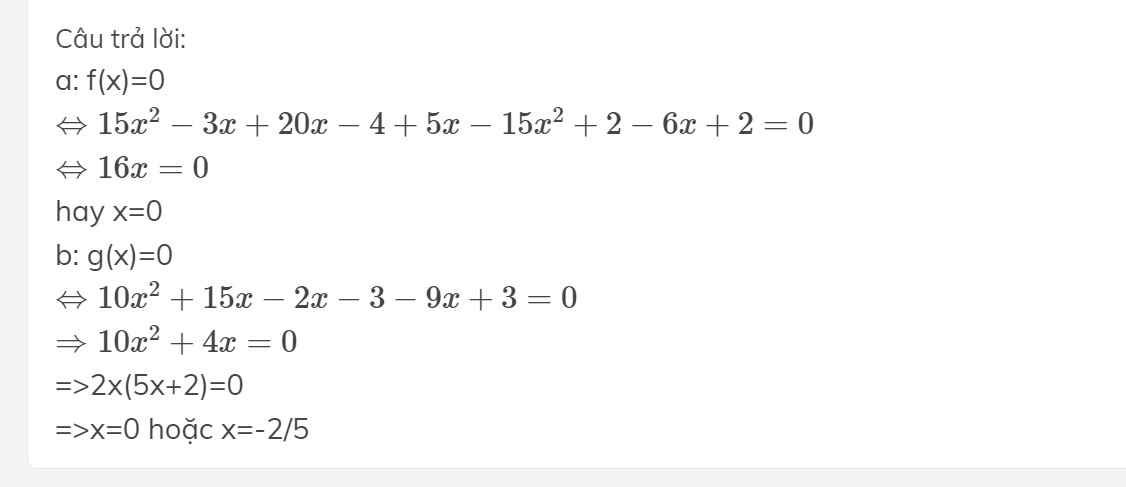
\(\left(1-3x\right)+\left(x-3\right)=\left(5x-1\right)-\left(5x+3\right)\)
\(\Rightarrow1-3x+x-3=5x-1-5x-3\)
\(\Rightarrow\left(1-3\right)-\left(3x-x\right)=\left(5x-5x\right)-\left(1+3\right)\)
\(\Rightarrow-2-2x=-4\)
\(\Rightarrow2x=-2+4\)
\(\Rightarrow2x=2\)
\(\Rightarrow x=1\)
Vậy \(x=1\)